THE FOUR KNIGHTS' TOURS

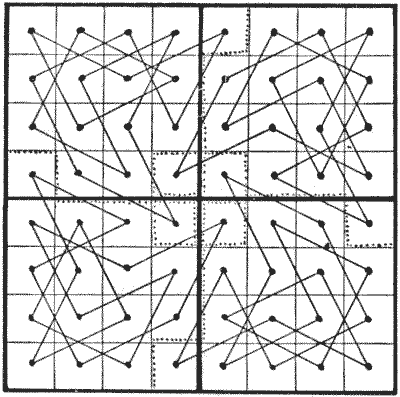I will repeat that if a chessboard be cut into four equal parts, as indicated by the dark lines in the illustration, it is not possible to perform a knight's tour, either re-entrant or not, on one of the parts. The best re-entrant attempt is shown, in which each knight has to trespass twice on other parts. The puzzle is to cut the board differently into four parts, each of the same size and shape, so that a re-entrant knight's tour may be made on each part. Cuts along the dotted lines will not do, as the four central squares of the board would be either detached or hanging on by a mere thread.