THE CROSS OF CARDS

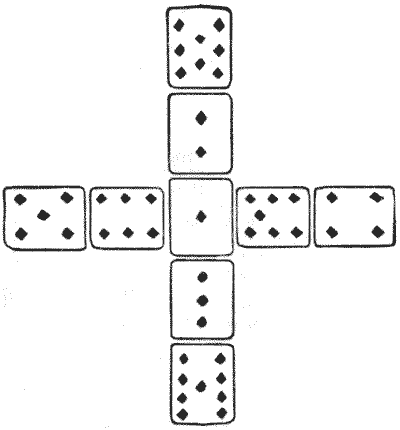In this case we use only nine cards—the ace to nine of diamonds. The puzzle is to arrange them in the form of a cross, exactly in the way shown in the illustration, so that the pips in the vertical bar and in the horizontal bar add up alike. In the example given it will be found that both directions add up `23`. What I want to know is, how many different ways are there of rearranging the cards in order to bring about this result? It will be seen that, without affecting the solution, we may exchange the `5` with the `6`, the `5` with the `7`, the `8` with the `3`, and so on. Also we may make the horizontal and the vertical bars change places. But such obvious manipulations as these are not to be regarded as different solutions. They are all mere variations of one fundamental solution. Now, how many of these fundamentally different solutions are there? The pips need not, of course, always add up `23`.