צלב הקלפים

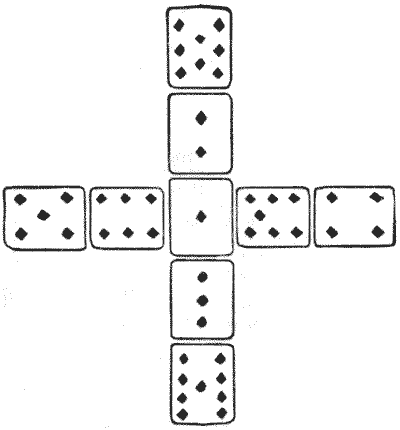במקרה זה אנו משתמשים רק בתשעה קלפים - האס עד תשע יהלומים. החידה היא לסדר אותם בצורת צלב, בדיוק כפי שמוצג באיור, כך שהנקודות בפס האנכי ובפס האופקי יסתכמו באופן שווה. בדוגמה הנתונה, ניתן לראות ששני הכיוונים מסתכמים ל-`23`. מה שאני רוצה לדעת הוא, כמה דרכים שונות יש לסדר מחדש את הקלפים כדי להגיע לתוצאה זו? ניתן לראות כי, מבלי להשפיע על הפתרון, אנו יכולים להחליף את ה-`5` עם ה-`6`, את ה-`5` עם ה-`7`, את ה-`8` עם ה-`3`, וכן הלאה. כמו כן, אנו יכולים לגרום לפסים האופקי והאנכי להחליף מקומות. אבל מניפולציות ברורות כאלה אינן נחשבות לפתרונות שונים. כולן וריאציות בלבד של פתרון יסודי אחד. עכשיו, כמה פתרונות שונים באופן מהותי כאלה יש? הנקודות לא צריכות, כמובן, תמיד להסתכם ל-`23`.