Number Theory, Division

Division is one of the four basic arithmetic operations, representing the splitting of a quantity into equal parts or finding how many times one number is contained within another. Questions involve performing division, understanding concepts like dividend, divisor, quotient, and remainder, and solving related word problems.

Parity (Even/Odd)

  • SIMPLE DIVISION

    Sometimes a very simple question in elementary arithmetic will cause a good deal of perplexity. For example, I want to divide the four numbers, `701, 1,059, 1,417`, and `2,312`, by the largest number possible that will leave the same remainder in every case. How am I to set to work Of course, by a laborious system of trial one can in time discover the answer, but there is quite a simple method of doing it if you can only find it. Sources:

  • A DORMITORY PUZZLE

    In a certain convent there were eight large dormitories on one floor, approached by a spiral staircase in the centre, as shown in our plan. On an inspection one Monday by the abbess it was found that the south aspect was so much preferred that six times as many nuns slept on the south side as on each of the other three sides. She objected to this overcrowding, and ordered that it should be reduced. On Tuesday she found that five times as many slept on the south side as on each of the other sides. Again she complained. On Wednesday she found four times as many on the south side, on Thursday three times as many, and on Friday twice as many. Urging the nuns to further efforts, she was pleased to find on Saturday that an equal number slept on each of the four sides of the house. What is the smallest number of nuns there could have been, and how might they have arranged themselves on each of the six nights? No room may ever be unoccupied.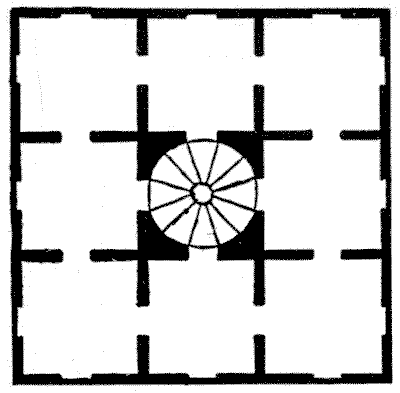 Sources:

  • THE BARRELS OF HONEY

     

    Once upon a time there was an aged merchant of Bagdad who was much respected by all who knew him. He had three sons, and it was a rule of his life to treat them all exactly alike. Whenever one received a present, the other two were each given one of equal value. One day this worthy man fell sick and died, bequeathing all his possessions to his three sons in equal shares.

    The only difficulty that arose was over the stock of honey. There were exactly twenty-one barrels. The old man had left instructions that not only should every son receive an equal quantity of honey, but should receive exactly the same number of barrels, and that no honey should be transferred from barrel to barrel on account of the waste involved. Now, as seven of these barrels were full of honey, seven were half-full, and seven were empty, this was found to be quite a puzzle, especially as each brother objected to taking more than four barrels of, the same description—full, half-full, or empty. Can you show how they succeeded in making a correct division of the property?

    Sources: