THE ROOK'S JOURNEY
This puzzle I call "The Rook's Journey," because the word "tour" (derived from a turner's wheel) implies that we return to the point from which we set out, and we do not do this in the present case. We should not be satisfied with a personally conducted holiday tour that ended by leaving us, say, in the middle of the Sahara. The rook here makes twenty-one moves, in the course of which journey it visits every square of the board once and only once, stopping at the square marked `10` at the end of its tenth move, and ending at the square marked `21`. Two consecutive moves cannot be made in the same direction—that is to say, you must make a turn after every move. 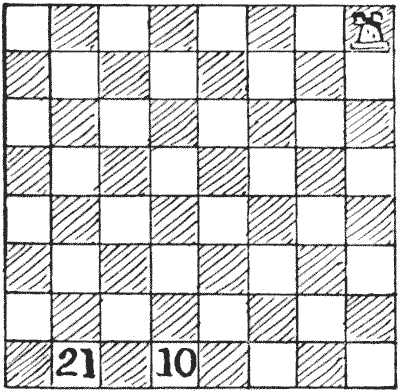

Topics:
Logic
->
Reasoning / Logic
Combinatorics
->
Case Analysis / Checking Cases
->
Processes / Procedures
Combinatorics
->
Combinatorial Geometry
->
Grid Paper Geometry / Lattice Geometry
Puzzles and Rebuses
- Amusements in Mathematics, Henry Ernest Dudeney Question 321
There are no comments yet.