Logic

Logic is the study of reasoning and valid inference. It involves analyzing statements, arguments, and deductive processes. Questions may include solving logic puzzles, evaluating the truth of compound statements, using truth tables, and identifying logical fallacies.

• Perpendicular Hands

  How many times a day do the hour and minute hands lie on the same line, forming an angle of `180^@`? Are any of these lines perpendicular to each other?

  Topics:

  Logic Proof and Example -> Proof by Contradiction Geometry -> Plane Geometry -> Angle Calculation

• A PUZZLE FOR CARD-PLAYERS

  Twelve members of a club arranged to play bridge together on eleven evenings, but no player was ever to have the same partner more than once, or the same opponent more than twice. Can you draw up a scheme showing how they may all sit down at three tables every evening? Call the twelve players by the first twelve letters of the alphabet and try to group them.
  Topics:

  Combinatorics Logic
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 265

• THE COLOURED COUNTERS

  The diagram represents twenty-five coloured counters, Red, Blue, Yellow, Orange, and Green (indicated by their initials), and there are five of each colour, numbered `1, 2, 3, 4`, and `5`. The problem is so to place them in a square that neither colour nor number shall be found repeated in any one of the five rows, five columns, and two diagonals. Can you so rearrange them?
  Topics:

  Combinatorics Logic Puzzles and Rebuses
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 307

• THE MANDARIN'S "T" PUZZLE

   

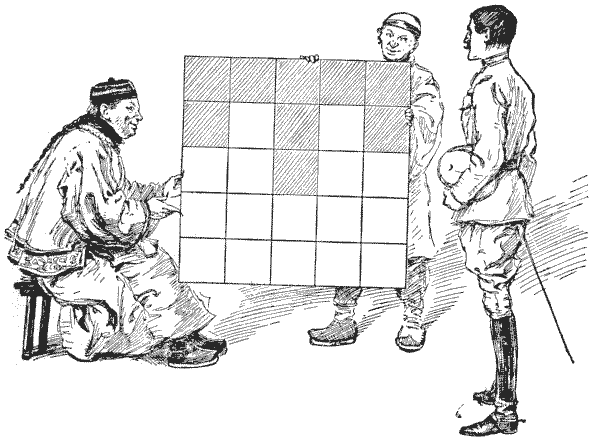
  Before Mr. Beauchamp Cholmondely Marjoribanks set out on his tour in the Far East, he prided himself on his knowledge of magic squares, a subject that he had made his special hobby; but he soon discovered that he had never really touched more than the fringe of the subject, and that the wily Chinee could beat him easily. I present a little problem that one learned mandarin propounded to our traveller, as depicted on the last page.

  The Chinaman, after remarking that the construction of the ordinary magic square of twenty-five cells is "too velly muchee easy," asked our countryman so to place the numbers `1` to `25` in the square that every column, every row, and each of the two diagonals should add up `65`, with only prime numbers on the shaded "T." Of course the prime numbers available are `1, 2, 3, 5, 7, 11, 13, 17, 19`, and `23`, so you are at liberty to select any nine of these that will serve your purpose. Can you construct this curious little magic square?

  Topics:

  Number Theory -> Prime Numbers Arithmetic Combinatorics Logic Puzzles and Rebuses
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 410

• THE MAGIC KNIGHT'S TOUR

  Here is a problem that has never yet been solved, nor has its impossibility been demonstrated. Play the knight once to every square of the chessboard in a complete tour, numbering the squares in the order visited, so that when completed the square shall be "magic," adding up to `260` in every column, every row, and each of the two long diagonals. I shall give the best answer that I have been able to obtain, in which there is a slight error in the diagonals alone. Can a perfect solution be found? I am convinced that it cannot, but it is only a "pious opinion."

  Topics:

  Logic Combinatorics -> Number Tables Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 412

• Question

  A vendor has two rolls of fabric, each `36` meters long. He sells the fabric in pieces of `3` meters. How many times will the vendor need to cut the fabric?

  Topics:

  Arithmetic Algebra -> Word Problems Logic -> Reasoning / Logic Number Theory -> Division
  Sources:
  • problems.ru web site

• Question

  Samuel has three sons, and each son has one sister. How many children are there in this family?

  Topics:

  Algebra -> Word Problems Logic -> Reasoning / Logic

• Question

  Two workers pave two kilometers of road within two days. How many workers are needed to pave `20` kilometers of road within `20` days?

  Topics:

  Arithmetic Algebra -> Equations Algebra -> Word Problems Logic -> Reasoning / Logic Number Theory -> Division

• Question

  In Danny's class there are `30` students. Danny claims that the number of boys is greater by `3` than the number of girls. Is it possible that Danny is right?

  Topics:

  Arithmetic Algebra -> Equations Algebra -> Word Problems Logic -> Reasoning / Logic Number Theory -> Division -> Parity (Even/Odd)

• Question

  If it is raining in Tel Aviv at `12` noon, is it possible that in `36` hours there will be sunshine in Tel Aviv?

  Topics:

  Logic -> Reasoning / Logic