Number Theory, Modular Arithmetic / Remainder Arithmetic

Modular Arithmetic (or Remainder Arithmetic) is a system where numbers 'wrap around' after reaching a certain value, the modulus. It deals with congruences and remainders. Questions involve solving equations in modular systems, finding powers modulo `n`, and applications in patterns or cryptography.

• Question

  The numbers from 1 to `10^9` (inclusive) are written on the board. The numbers divisible by 3 are written in red, and the rest of the numbers are written in blue. The sum of all the red numbers is equal to `X`, and the sum of all the blue numbers is equal to `Y`. Which number is larger, `2X` or `Y`, and by how much?

  Topics:

  Arithmetic Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules -> Divisibility Rules by 3 and 9 Logic -> Reasoning / Logic Algebra -> Sequences Algebra -> Inequalities -> Averages / Means Number Theory -> Division
  Sources:
  • Beno Arbel Olympiad, 2017, Grade 8 Question 2

• THE BARREL OF BEER

  A man bought an odd lot of wine in barrels and one barrel containing beer. These are shown in the illustration, marked with the number of gallons that each barrel contained. He sold a quantity of the wine to one man and twice the quantity to another, but kept the beer to himself. The puzzle is to point out which barrel contains beer. Can you say which one it is? Of course, the man sold the barrels just as he bought them, without manipulating in any way the content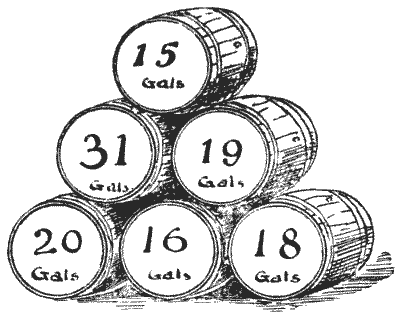s.
  Topics:

  Arithmetic Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules -> Divisibility Rules by 3 and 9 Algebra -> Word Problems Logic -> Reasoning / Logic
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 76

• DIGITAL DIVISION

  It is another good puzzle so to arrange the nine digits (the nought excluded) into two groups so that one group when divided by the other produces a given number without remainder. For example, `1` `3` `4` `5` `8` divided by `6` `7` `2` `9` gives `2`. Can the reader find similar arrangements producing `3, 4, 5, 6, 7, 8`, and `9` respectively? Also, can he find the pairs of smallest possible numbers in each case? Thus, `1` `4` `6` `5` `8` divided by `7` `3` `2` `9` is just as correct for `2` as the other example we have given, but the numbers are higher.
  Topics:

  Arithmetic Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules -> Divisibility Rules by 3 and 9 Number Theory -> Division
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 88

• SLV LVS BLS

  In the following expression, different letters represent different digits, and identical letters represent identical digits:

  SLV = LVS + BLS

  Find the number SLV.

  Topics:

  Arithmetic Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules -> Divisibility Rule by 11 Algebra -> Equations Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Puzzles and Rebuses -> Reconstruct the Exercise / Cryptarithmetic
  Sources:
  • Young Mathematician Olympiad, 2019-2020, Stage B, Grades 5-6 Question 3

• Question

  Find the largest natural number in which all digits are distinct, and if you look at every 3 consecutive digits, you get a number divisible by 13.

  Topics:

  Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules -> Divisibility Rule by 11 Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures
  Sources:
  • Beno Arbel Olympiad, 2017, Grade 8 Question 7

• THE MYSTIC ELEVEN

  Can you find the largest possible number containing any nine of the ten digits (calling nought a digit) that can be divided by `11` without a remainder? Can you also find the smallest possible number produced in the same way that is divisible by `11`? Here is an example, where the digit `5` has been omitted: `896743012`. This number contains nine of the digits and is divisible by `11`, but it is neither the largest nor the smallest number that will work.

  Topics:

  Arithmetic Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules -> Divisibility Rule by 11
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 93

• THE BANKER'S PUZZLE

  A banker had a sporting customer who was always anxious to wager on anything. Hoping to cure him of his bad habit, he proposed as a wager that the customer would not be able to divide up the contents of a box containing only sixpences into an exact number of equal piles of sixpences. The banker was first to put in one or more sixpences (as many as he liked); then the customer was to put in one or more (but in his case not more than a pound in value), neither knowing what the other put in. Lastly, the customer was to transfer from the banker's counter to the box as many sixpences as the banker desired him to put in. The puzzle is to find how many sixpences the banker should first put in and how many he should ask the customer to transfer, so that he may have the best chance of winning.
  Topics:

  Number Theory -> Prime Numbers Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Euler's Theorem and Fermat's Little Theorem
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 134

• Question

  a. Prove that among `11` natural numbers, it is always possible to choose two such that their units digit is the same.

  b. Prove that among `11` natural numbers, it is always possible to choose two such that their difference is divisible by `10`.

  Topics:

  Combinatorics -> Pigeonhole Principle Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules -> Divisibility Rules by 5 and 25