חמש אבני דומינו

 

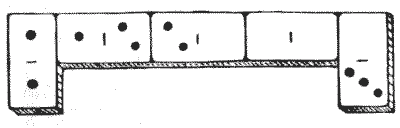
הנה חידה קטנה חדשה שאינה קשה, אך כנראה תמצא חן בעיני הקוראים שלי. ניתן לראות שחמש אבני הדומינו מסודרות ברצף נכון (כלומר, עם `1` כנגד `1, 2` כנגד `2`, וכן הלאה), כך שהמספר הכולל של הנקודות בשתי אבני הדומינו הקיצוניות הוא חמש, וסכום הנקודות בשלוש אבני הדומינו באמצע הוא גם חמש. ישנן רק שלוש סידורים אחרים שנותנים חמש עבור הסכומים. הם: —

(1—0) (0—0) (0—2) (2—1) (1—3)
(4—0) (0—0) (0—2) (2—1) (1—0)
(2—0) (0—0) (0—1) (1—3) (3—0)

עכשיו, כמה סידורים דומים יש לחמש אבני דומינו שייתנו שש במקום חמש בשני הסכומים?


נושאים:
קומבינטוריקה -> בדיקת מקרים -> תהליכים
מקורות:
עדיין אין תגובות.
נדרש אימות

יש להתחבר על מנת לשלוח תגובה.

כניסה