Frame

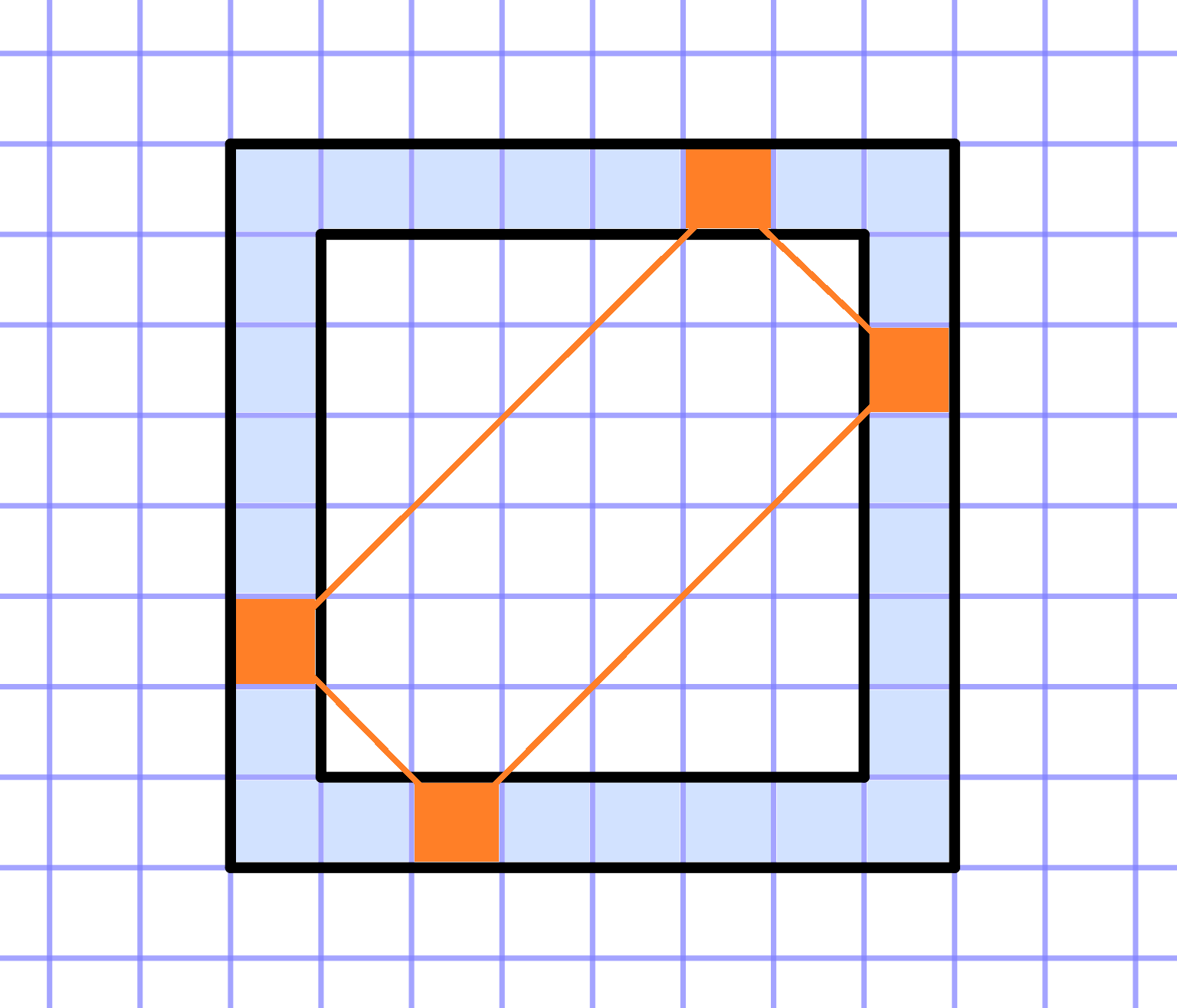
On a grid paper, a square of size `NxxN` is given. Consider its frame with a width of one square. It consists of `4*(N-1)` squares.

Can you write `4*(N-1)` consecutive integers (not necessarily positive) in the squares of the frame, such that the following condition holds:

For every rectangle whose vertices are on the frame and whose sides are parallel to the diagonals of the original square, the sum of the numbers at the vertices is equal to a constant value. This also includes the "degenerate" rectangles of zero width that coincide with the diagonals of the square - in this case, simply sum the two numbers at the opposite vertices of the square.

For:

a. `N=3`

b. `N=4`

c. `N=5`