Algebra, Sequences, Arithmetic Progression / Arithmetic Sequence

An arithmetic sequence is one where the difference between consecutive terms is constant (this constant is called the common difference). Questions involve finding the `n`-th term, the sum of the first `n` terms, the common difference, or other properties based on given information.

• Continue the Sequence

  `2, 6, 12, 20, 30…`

  a. What is the next number (the sixth) in the sequence?

  b. What is the `2016`th number in the sequence?

  Topics:

  Arithmetic Logic -> Reasoning / Logic Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence Algebra -> Sequences -> Complete/Continue the Sequence
  Sources:
  • problems.ru web site

• Question

  Given a positive integer N, consider the following process: Let `S(N)` denote the sum of the digits of N. Take the sum of the digits of `S(N)`. Repeat this operation until a single-digit number is obtained. We call the number of times we performed the above process until we obtained a single-digit number the "depth" of N. For example, the depth of 49 is `S(49)=13 -> S(13)=4`, the operation was performed twice (and the depth of 45 is 1).

  a) Prove that for every number N there is indeed a finite depth, that is, a single-digit number is always obtained at some stage of the process.

  b) Let `x(n)` denote the minimum number (with the smallest value) with depth N. Find the remainder of `x(5776)` when divided by 6. Justify your answer!

  c) Find the remainder of the number `x(5776) - x(5708)` when divided by 2016. Justify your answer!

  Show hint

  Log in here to receive the hint
  Topics:

  Number Theory -> Modular Arithmetic / Remainder Arithmetic Combinatorics -> Induction (Mathematical Induction) Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence
  Sources:
  • Gillis Mathematical Olympiad, 2015-2016 Question 3

• Question

  Find the sum of all natural numbers from `1` to `100`.

  Topics:

  Arithmetic Algebra -> Algebraic Techniques Logic -> Reasoning / Logic Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence

• Question

  The following numbers are written on the board: `1, 2, 3, …, 2016, 2017`. In one move, it is allowed to choose a pair of numbers written on the board, erase them, and write their (positive) difference in their place. After several such operations, a single number remains on the board. Is it possible that this is zero?

  Topics:

  Arithmetic Combinatorics -> Invariants Combinatorics -> Induction (Mathematical Induction) Number Theory -> Division -> Parity (Even/Odd) Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Proof and Example -> Proof by Contradiction

• Question

  Does there exist an infinite arithmetic progression consisting only of prime numbers?

  Note: We do not consider "trivial" arithmetic progressions, which are constant.

  Show hint

  Log in here to receive the hint
  Topics:

  Number Theory -> Prime Numbers Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence Proof and Example -> Proof by Contradiction

• Question

  By how much is the sum of all even numbers not exceeding `100` greater than the sum of all odd numbers not exceeding `100`?

  Topics:

  Arithmetic Combinatorics -> Double Counting Algebra -> Algebraic Techniques Logic -> Reasoning / Logic Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence

• Question

  Prove that 

  `1+3+5+...+(2n-1)=n^2`

  Topics:

  Combinatorics -> Induction (Mathematical Induction) Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence

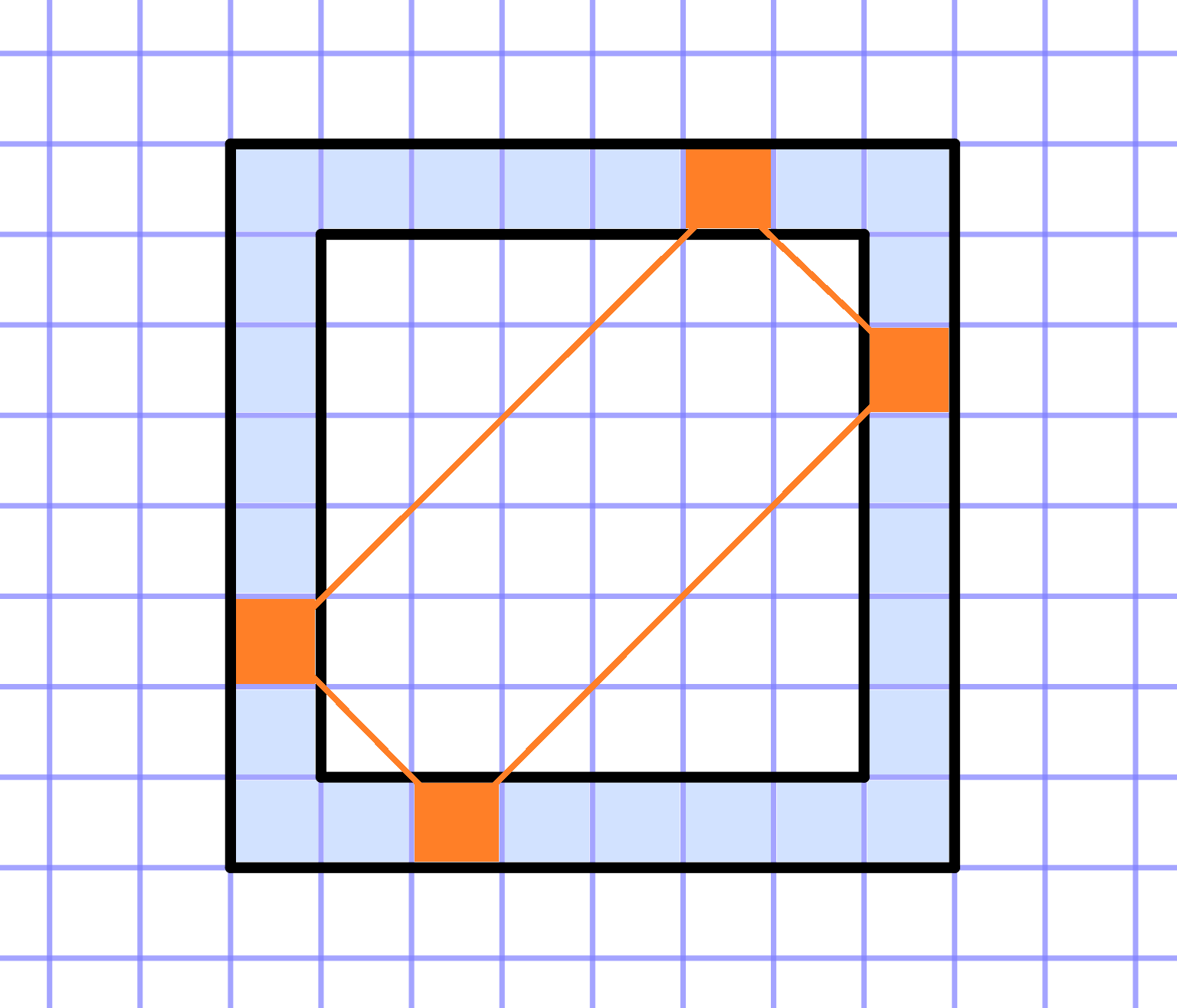
• Frame

  On a grid paper, a square of size `NxxN` is given. Consider its frame with a width of one square. It consists of `4*(N-1)` squares.

  Can you write `4*(N-1)` consecutive integers (not necessarily positive) in the squares of the frame, such that the following condition holds:

  For every rectangle whose vertices are on the frame and whose sides are parallel to the diagonals of the original square, the sum of the numbers at the vertices is equal to a constant value. This also includes the "degenerate" rectangles of zero width that coincide with the diagonals of the square - in this case, simply sum the two numbers at the opposite vertices of the square.

  For:

  a. `N=3`

  b. `N=4`

  c. `N=5`

  

  Topics:

  Arithmetic Number Theory -> Division -> Parity (Even/Odd) Proof and Example -> Constructing an Example / Counterexample Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures
  Sources:
  • Tournament of Towns, 1983-1984, Fall, Practice Version, Grades 9-10 Question 3 Points 2+3+4

• Question

  `120` identical spheres are arranged in the shape of a triangular pyramid. How many layers are there in the pyramid?

  Note: This is a pyramid, which is a three-dimensional shape, and not a triangle in a plane.

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Solid Geometry / Geometry in Space Arithmetic Logic -> Reasoning / Logic Proof and Example -> Constructing an Example / Counterexample Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence Algebra -> Sequences -> Complete/Continue the Sequence Number Theory -> Triangular Numbers

• Question

  Given the sequence `1 , 1/2 ,1/3 ,1/4 ,1/5,...`, does there exist an arithmetic sequence composed of terms from the aforementioned sequence?

  1. Of length 5

  2. Of any length

  Show hint

  Log in here to receive the hint
  Topics:

  Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules Proof and Example -> Constructing an Example / Counterexample Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence Arithmetic -> Fractions Number Theory -> Greatest Common Divisor (GCD) and Least Common Multiple (LCM)
  Sources:
  • Tournament of Towns, 1981-1982, Spring