Proof and Example

This category emphasizes the core mathematical activities of constructing rigorous arguments (proofs) to establish general truths, and using specific instances (examples) to illustrate concepts, test conjectures, or find counterexamples. Questions may ask for either or both.

• Question

  Prove that for every prime number `p>3 ` the following holds: `p^2-1` is divisible by `6`.

  Topics:

  Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules Algebra -> Algebraic Techniques -> Short Multiplication Formulas / Algebraic Identities Number Theory -> Division -> Parity (Even/Odd) Proof and Example Number Theory -> Prime Numbers -> Prime Factorization

• Question

  Prove that any real number can be written as the sum of 9 numbers, each of which is composed only of the digits 0 and 7.

  Topics:

  Number Theory Arithmetic Proof and Example Algebra -> Sequences
  Sources:
  • Tournament of Towns, 1980-1981, Spring, Main Version, Grades 11-12 Question 3

• Question

  Prove that the product of two consecutive numbers is always even.

  Topics:

  Number Theory -> Division -> Parity (Even/Odd) Proof and Example

• Question

  Given a real number `a` such that `a+1/a` is an integer. Prove that `a^2+1/a^2` is also an integer.

  Topics:

  Algebra -> Algebraic Techniques Algebra -> Equations Proof and Example

• Question

  Given a real number `a` such that `a+1/a` is an integer. Prove that `a^n+1/a^n` is also an integer for every natural number `n`.

  Topics:

  Number Theory Combinatorics -> Induction (Mathematical Induction) Algebra -> Algebraic Techniques Proof and Example Algebra -> Sequences

• Question

  Two congruent triangles form a Star of David as depicted in the drawing. Prove that the shaded area is equal to the hatched area.

  

  Show hint

  Log in here to receive the hint
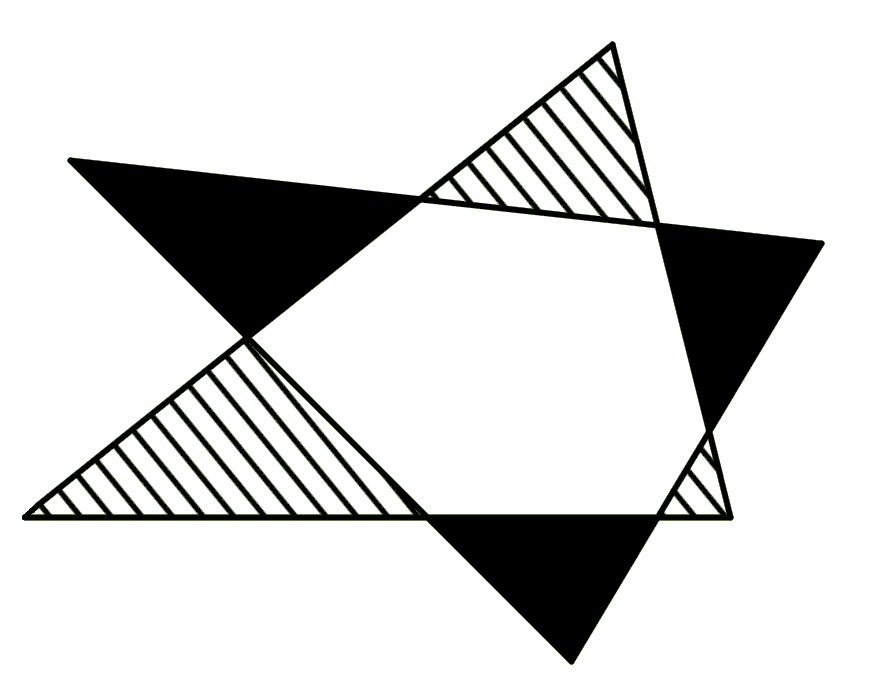  Topics:

  Geometry -> Area Calculation Proof and Example Set Theory Geometry -> Plane Geometry -> Triangles -> Triangle Congruence

• Question

  Can you cut the shape on the left into six shapes like the shape on the right?

  

  Topics:

  Combinatorics -> Invariants Combinatorics -> Matchings Proof and Example Combinatorics -> Colorings -> Chessboard Coloring Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry

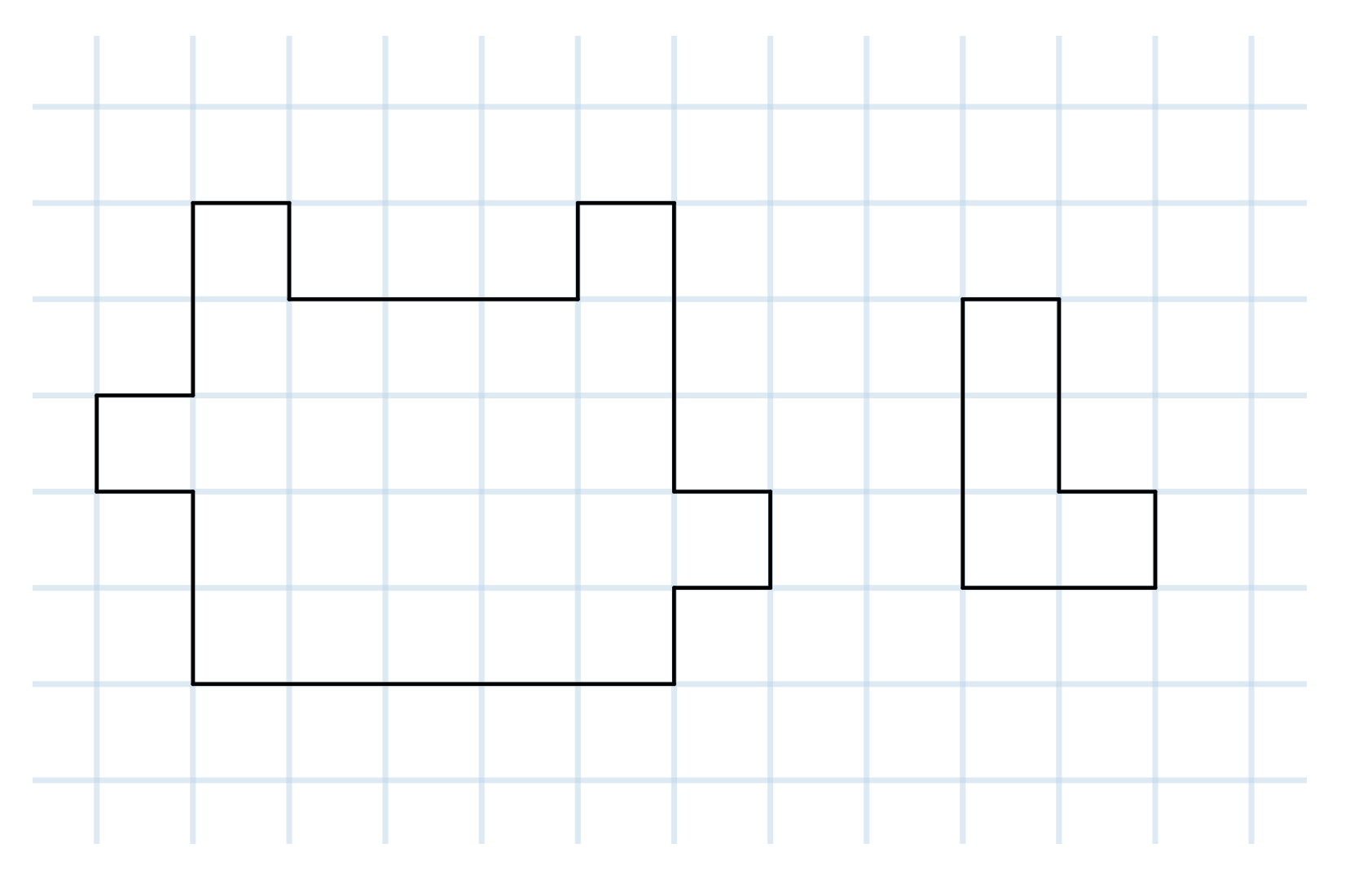
• Question

  Prove that the sum of two consecutive numbers is always odd.

  Topics:

  Number Theory -> Division -> Parity (Even/Odd) Proof and Example

• Question

  Given two numbers such that one is obtained from the other by changing the order of its digits. Prove that their difference is divisible by `9`.

  Topics:

  Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules -> Divisibility Rules by 3 and 9 Proof and Example Arithmetic -> Division with Remainder

• Question

  Given a natural number `n` that is three times greater than the sum of its digits. Prove that `n` is divisible by `27`.

  Topics:

  Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules -> Divisibility Rules by 3 and 9 Proof and Example