השולחן והשרפרפים

הזדמן לי לא פעם להראות שהתשובות שפורסמו למספר רב של החידות העתיקות והידועות ביותר הן שגויות לחלוטין או ניתנות לשיפור. אני מציע לשקול את החידה הישנה של השולחן והשרפרפים שרוב הקוראים שלי ראו כנראה בצורה זו או אחרת בספרים שנערכו לשעשוע הילדות.

הסיפור מספר שמנהל בית ספר חסכן ובעל תושייה רצה פעם להפוך משטח שולחן עגול, שלא היה לו שימוש בו, למושבים עבור שני שרפרפים אובליים, שלכל אחד מהם חור אחיזה במרכז. הוא הורה לנגר לבצע את החיתוכים כפי שמוצג באיור ולאחר מכן לחבר את שמונת החלקים יחד באופן המוצג. הוא התרשם כל כך מהתושייה שבהופעתו, שהוא הציג את החידה לכיתת הגיאומטריה שלו כלימוד קטן בניתוח. אבל המשך הסיפור מעולם לא פורסם, מכיוון שלפי השמועה, היה זה אופייני למנהלי האקדמיות שהם לעולם לא יודו שהם יכולים לטעות. אני מקבל את המידע שלי מצאצא של הילד המקורי שהיה לו הכי הרבה סיבות להתעניין בעניין.

הצעיר החכם הציע בענווה למורה שחורי האחיזה גדולים מדי, וייתכן שילד קטן עלול ליפול דרכם. לכן הוא הציע דרך נוספת לבצע את החיתוכים שתתגבר על ההתנגדות הזו. על חוצפתו הוא קיבל עונש כה חמור שהוא השתכנע שככל שחור האחיזה בשרפרפים גדול יותר, כך הם עלולים להיות נוחים יותר. 

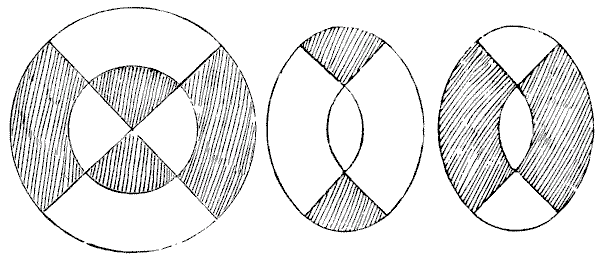
מה הייתה השיטה שהילד הציע?

האם אתה יכול להראות כיצד ניתן לחתוך את משטח השולחן העגול לשמונה חלקים שיתאימו זה לזה וייצרו שני מושבים אובליים לשרפרפים (כל אחד באותו גודל וצורה בדיוק) ולכל אחד מהם חורי אחיזה דומים במידות קטנות יותר מאשר במקרה המוצג לעיל? כמובן, יש להשתמש בכל העץ.