חידת חמשת הכלבים

בשנת `1863`, סי. אף. דה יאניש דן לראשונה ב"חידת חמש המלכות" - להציב חמש מלכות על לוח השחמט כך שכל משבצת תותקף או תאוכלס - אשר הוצעה על ידי חברו, "מר דה ר.". יאניש הראה שאם אף מלכה לא יכולה לתקוף מלכה אחרת, ישנן תשעים ואחת דרכים שונות להציב את חמש המלכות, כאשר היפוכים ושיקופים אינם נחשבים כשונים. אם המלכות יכולות לתקוף זו את זו, תיעדתי מאות דרכים, אך לא ניתן למנות אותן במדויק. 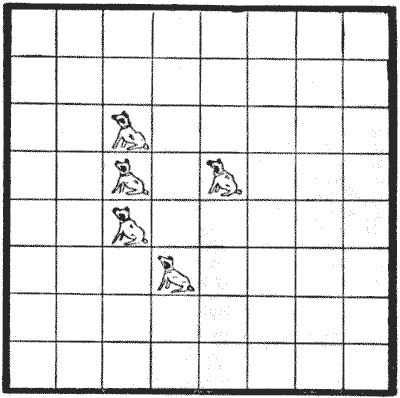האיור אמור לייצג סידור של שישים וארבעה מְלוּנוֹת. ניתן לראות שחמש מְלוּנוֹת מכילות כל אחת כלב, ובבדיקה נוספת ניתן לראות שכל אחת משישים וארבע המְלוּנוֹת נמצאת בקו ישר עם לפחות כלב אחד - או אופקית, אנכית או באלכסון. קח כל מְלוּנָה שתרצה, ותגלה שתוכל למתוח קו ישר לכלב באחת משלוש הדרכים שהוזכרו. החידה היא להחליף את חמשת הכלבים ולגלות בכמה דרכים שונות ניתן להציב אותם בחמש מְלוּנוֹת בשורה ישרה, כך שכל מְלוּנָה תמיד תהיה בקו אחד עם לפחות כלב אחד. היפוכים ושיקופים נחשבים כאן כשונים.