Puzzles and Rebuses, Matchstick Puzzles

Matchstick puzzles involve arranging or moving a small number of matchsticks to achieve a specific goal, such as forming a certain number of shapes (squares, triangles), correcting an arithmetic equation, or creating a particular pattern. They test spatial reasoning and ingenuity.

• Question

  Move one matchstick to make a valid equation.

  

  Note: There may be multiple solutions.

  Topics:

  Arithmetic Puzzles and Rebuses -> Matchstick Puzzles
  Sources:
  • Tournament of Towns, 1983-1984, Fall, Practice Version, Grades 9-10 Question 4 Points 8

• The Matchstick Root

  Move one matchstick to make a correct equality:

  

  Topics:

  Algebra -> Algebraic Techniques -> Roots / Radicals Puzzles and Rebuses -> Matchstick Puzzles

• 5 Squares

  Move three matches to create 5 squares:

  

  Topics:

  Puzzles and Rebuses -> Matchstick Puzzles

• 8-5=7?

  Remove two matchsticks to make the following equation true:

  

  Topics:

  Puzzles and Rebuses -> Matchstick Puzzles
  Sources:
  • problems.ru web site

• Inverted Chair

  The chair is upside down. You need to move two matchsticks to return it to its original position.

  

  Topics:

  Puzzles and Rebuses -> Matchstick Puzzles

• Add 2, Get 4

  Add 2 matchsticks to form exactly 4 squares:

  

  Topics:

  Puzzles and Rebuses -> Matchstick Puzzles

• A NEW MATCH PUZZLE

  In the illustration eighteen matches are shown arranged so that they enclose two spaces, one just twice as large as the other. Can you rearrange them (`1`) so as to enclose two four-sided spaces, one exactly three times as large as the other, and (`2`) so as to enclose two five-sided spaces, one exactly three times as large as the other? All the eighteen matches must be fairly used in each case; the two spaces must be quite detached, and there must be no loose ends or duplicated matches.
  Topics:

  Geometry -> Area Calculation Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Puzzles and Rebuses -> Matchstick Puzzles
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 204

• THE SIX SHEEP-PENS

   

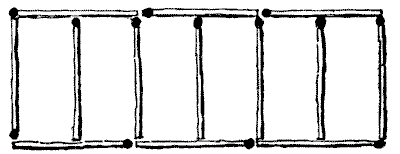
  Here is a new little puzzle with matches. It will be seen in the illustration that thirteen matches, representing a farmer's hurdles, have been so placed that they enclose six sheep-pens all of the same size. Now, one of these hurdles was stolen, and the farmer wanted still to enclose six pens of equal size with the remaining twelve. How was he to do it? All the twelve matches must be fairly used, and there must be no duplicated matches or loose ends.

  Topics:

  Puzzles and Rebuses -> Matchstick Puzzles
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 205

• THE SIXTEEN SHEEP

  Here is a new puzzle with matches and counters or coins. In the illustration the matches represent hurdles and the counters sheep. The sixteen hurdles on the outside, and the sheep, must be regarded as immovable; the puzzle has to do entirely with the nine hurdles on the inside. It will be seen that at present these nine hurdles enclose four groups of `8, 3, 3`, and `2` sheep. The farmer requires to readjust some of the hurdles so as to enclose `6, 6`, and `4` sheep. Can you do it by only replacing two hurdles? When you have succeeded, then try to do it by replacing three hurdles; then four, five, six, and seven in succession. Of course, the hurdles must be legitimately laid on the dotted lines, and no such tricks are allowed as leaving unconnected ends of hurdles, or two hurdles placed side by side, or merely making hurdles change places. In fact, the conditions are so simple that any farm labourer will understand it directly.
  Topics:

  Puzzles and Rebuses -> Matchstick Puzzles
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 275