Geometry, Area Calculation

This topic focuses on methods for determining the size of a two-dimensional surface or region. Questions involve calculating the areas of various geometric shapes like triangles, quadrilaterals, circles, and more complex composite figures, often requiring application of specific formulas.

• Question

  Given two squares, each with a side length of `3` centimeters, and joined together to form a rectangle, what is the perimeter of the resulting rectangle?

  Topics:

  Arithmetic Geometry -> Plane Geometry Geometry -> Area Calculation Algebra -> Word Problems

• Question

  Samuel wants to tile a room measuring `3` by `4` meters using square tiles with a side length of `25` centimeters. How many tiles does Samuel need?

  Topics:

  Arithmetic Geometry -> Area Calculation Algebra -> Word Problems Units of Measurement

• Question

  Given a convex quadrilateral ABCD. Each of its sides is divided into K equal parts. Points on side AB are connected to corresponding points on CD, and points on BC are connected to points on DA, creating K² smaller quadrilaterals. From these, K quadrilaterals are chosen such that any two quadrilaterals are separated by at least one line connecting AB and CD, and one line connecting BC and DA. Prove that the sum of the areas of these quadrilaterals is S_ABCD/K. 
  By A. Angans. 

  Topics:

  Geometry -> Plane Geometry Geometry -> Area Calculation Geometry -> Vectors
  Sources:
  • Tournament of Towns, 1979-1980, Main, Spring Question 5

• Question

  In a square with side length 1, a finite number of segments parallel to the sides of the square were drawn, with a total length of 18 (they can intersect). Prove that among the parts into which the square is divided by the segments, there is a part with an area of at least 0.01. 
  A. Engenes, A. Brazins 

  Topics:

  Geometry -> Plane Geometry Geometry -> Area Calculation Algebra -> Inequalities Proof and Example -> Proof by Contradiction
  Sources:
  • Tournament of Towns, 1979-1980, Main, Spring Question 6

• Question

  A regular polygon with 4k sides is divided into parallelograms. Prove that among these parallelograms there are at least k rectangles. Find the sum of the areas of all the rectangles.

  Topics:

  Geometry -> Plane Geometry Geometry -> Area Calculation Geometry -> Solid Geometry / Geometry in Space -> Polyhedra -> Regular Polyhedra

• Question

  Let ABCD be a convex quadrilateral inscribed in a circle such that its diagonals are perpendicular to each other. Let O be the center of the circle. Prove that the broken line AOC divides the quadrilateral into two parts of equal area. 
  V. Varvarkin 

  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Circles Geometry -> Plane Geometry -> Angle Calculation
  Sources:
  • Tournament of Towns, 1980-1981, Spring, Main Version, Grades 9-10 Question 3 Points 5

• Area and Perimeter

  By what percentage will the area of a square increase if its perimeter increases by `10%`?

  Topics:

  Geometry -> Area Calculation Arithmetic -> Percentages

• Stack of Papers

  Several identical rectangular sheets of paper lie on a table. It is known that the top sheet covers more than half the area of every other sheet. Is it necessarily possible to stick a pin into the table that will go through all these sheets?

  Topics:

  Combinatorics -> Pigeonhole Principle Combinatorics -> Combinatorial Geometry Geometry -> Area Calculation Geometry -> Plane Geometry -> Symmetry

• Question

  Semicircles are constructed on the legs and hypotenuse of a right-angled triangle, as shown in the figure. Which area is larger—the hatched area or the shaded area?

  

  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Triangles Geometry -> Plane Geometry -> Circles Geometry -> Plane Geometry -> Pythagorean Theorem

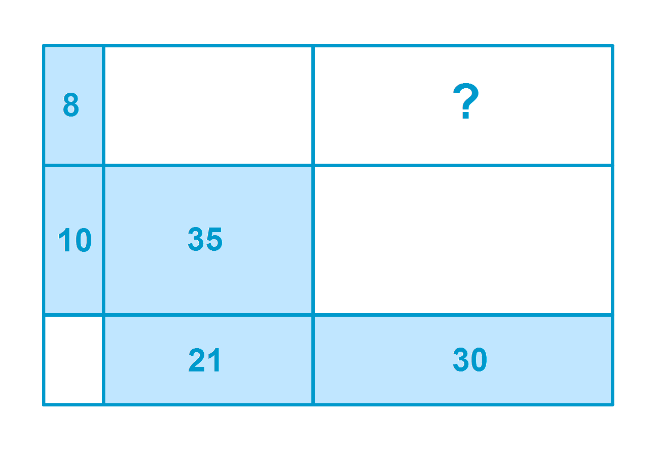
• Question

  Find the area marked by the question mark:

  

  Topics:

  Geometry -> Plane Geometry Geometry -> Area Calculation