חידת שרשרת

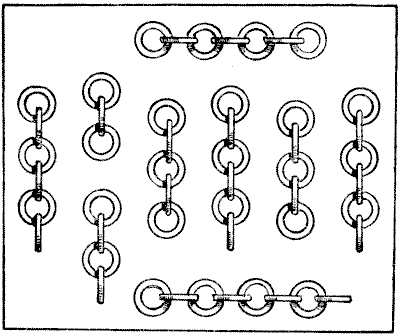זוהי חידה המבוססת על רעיון נחמד שבו עסק לראשונה מר סם לויד המנוח. לאיש היו תשעה חלקי שרשרת, כפי שמוצג באיור. הוא רצה לחבר את חמישים החוליות האלה לשרשרת אינסופית אחת. יעלה פרוטה לפתוח כל חוליה ושתי פרוטות לרתך חוליה בחזרה, אבל הוא יכול לקנות שרשרת אינסופית חדשה באותו אופי ואיכות עבור `2`s. `2`d. מה היה המהלך הזול ביותר עבורו? אלא אם כן הקורא ערמומי הוא עלול למצוא את עצמו רחוק מהתשובה.