צלבים של מוֹנִים
כל מה שאנחנו צריכים לפאזל הזה הם תשעה מוֹנִים, ממוספרים `1, 2, 3, 4, 5, 6, 7, 8` ו-`9`. ניתן לראות באיור A שהם מסודרים כך שיוצרים צלב יווני, ואילו במקרה של B הם יוצרים צלב לטיני. בשני המקרים הקורא יגלה שסכום המספרים באנך של הצלב זהה לסכום המספרים בזרוע האופקית. קל למדי להגיע לסידור כזה בניסוי וטעייה, אך הבעיה היא לגלות בדיוק בכמה דרכים שונות ניתן לעשות זאת בכל מקרה. זכרו שהיפוכים ושיקופים אינם נחשבים כשונים. כלומר, אם תסובבו את הדף הזה תקבלו ארבעה סידורים של הצלב היווני, ואם תסובבו אותו שוב מול מראה תקבלו ארבעה נוספים. אבל את שמונתם אלה מחשיבים כזהים. עכשיו, כמה דרכים שונות יש בכל מקרה? 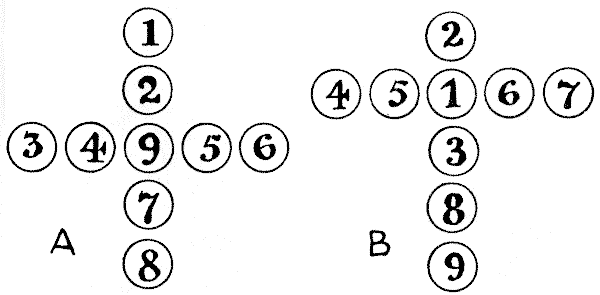
נושאים:
קומבינטוריקה
->
כלל המכפלה
קומבינטוריקה
->
בדיקת מקרים
->
תהליכים
קומבינטוריקה
->
טבלאות מספריות
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 277
עדיין אין תגובות.