סיור המלכה
החידה של ביצוע סיור שלם בלוח השחמט עם המלכה במספר המהלכים המועט ביותר האפשרי (שבו ניתן לבקר בריבועים יותר מפעם אחת) ניתנה לראשונה על ידי סם לויד המנוח ב-אסטרטגיית שחמט שלו. אבל הפתרון המוצג להלן הוא זה שהוא נתן ב-אגוזי שחמט אמריקאים ב-`1868`. תיעדתי לפחות שישה פתרונות שונים במספר המינימלי של מהלכים - ארבעה עשר - אבל זה הטוב מכולם, מסיבות שאסביר. 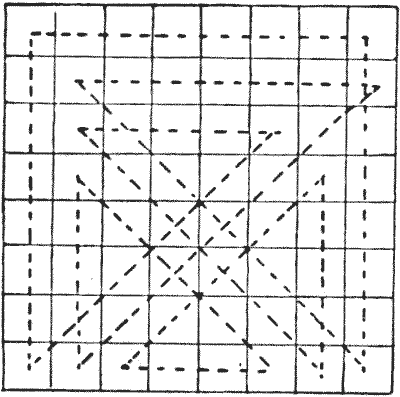 אם תסתכלו על הריבוע המסומן באותיות, תבינו שיש רק עשרה ריבועים שונים באמת בלוח שחמט - אלה התחומים בקו כהה - כל השאר הם רק היפוכים או שיקופים. לדוגמה, כל A הוא ריבוע פינתי, וכל J הוא ריבוע מרכזי. כתוצאה מכך, מכיוון שלפתרון המוצג יש נקודת מפנה בריבוע D התחום, אנו יכולים לקבל פתרון שמתחיל ומסתיים בכל ריבוע המסומן D - פשוט על ידי סיבוב הלוח. כעת, תוכנית זו תעניק לך סיור שמתחיל מכל A, B, C, D, E, F או H, בעוד שאף מסלול אחר שאני מכיר לא ניתן להתאמה ליותר מחמש נקודות התחלה שונות. אין סיור מלכה בארבעה עשר מהלכים (זכור שסיור חייב להיות חוזר) שיכול להתחיל מ-G, I או J. אבל יכולה להיות לנו דרך לא חוזרת על כל הלוח בארבעה עשר מהלכים, החל מכל ריבוע נתון. מכאן החידה הבאה: -
אם תסתכלו על הריבוע המסומן באותיות, תבינו שיש רק עשרה ריבועים שונים באמת בלוח שחמט - אלה התחומים בקו כהה - כל השאר הם רק היפוכים או שיקופים. לדוגמה, כל A הוא ריבוע פינתי, וכל J הוא ריבוע מרכזי. כתוצאה מכך, מכיוון שלפתרון המוצג יש נקודת מפנה בריבוע D התחום, אנו יכולים לקבל פתרון שמתחיל ומסתיים בכל ריבוע המסומן D - פשוט על ידי סיבוב הלוח. כעת, תוכנית זו תעניק לך סיור שמתחיל מכל A, B, C, D, E, F או H, בעוד שאף מסלול אחר שאני מכיר לא ניתן להתאמה ליותר מחמש נקודות התחלה שונות. אין סיור מלכה בארבעה עשר מהלכים (זכור שסיור חייב להיות חוזר) שיכול להתחיל מ-G, I או J. אבל יכולה להיות לנו דרך לא חוזרת על כל הלוח בארבעה עשר מהלכים, החל מכל ריבוע נתון. מכאן החידה הבאה: - 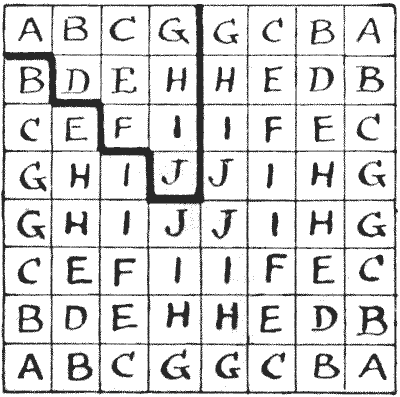 התחל מ-J בחלק הסגור של הדיאגרמה המסומנת באותיות ובקר בכל ריבוע בלוח בארבעה עשר מהלכים, וסיים היכן שתרצה.
התחל מ-J בחלק הסגור של הדיאגרמה המסומנת באותיות ובקר בכל ריבוע בלוח בארבעה עשר מהלכים, וסיים היכן שתרצה.
 אם תסתכלו על הריבוע המסומן באותיות, תבינו שיש רק עשרה ריבועים שונים באמת בלוח שחמט - אלה התחומים בקו כהה - כל השאר הם רק היפוכים או שיקופים. לדוגמה, כל A הוא ריבוע פינתי, וכל J הוא ריבוע מרכזי. כתוצאה מכך, מכיוון שלפתרון המוצג יש נקודת מפנה בריבוע D התחום, אנו יכולים לקבל פתרון שמתחיל ומסתיים בכל ריבוע המסומן D - פשוט על ידי סיבוב הלוח. כעת, תוכנית זו תעניק לך סיור שמתחיל מכל A, B, C, D, E, F או H, בעוד שאף מסלול אחר שאני מכיר לא ניתן להתאמה ליותר מחמש נקודות התחלה שונות. אין סיור מלכה בארבעה עשר מהלכים (זכור שסיור חייב להיות חוזר) שיכול להתחיל מ-G, I או J. אבל יכולה להיות לנו דרך לא חוזרת על כל הלוח בארבעה עשר מהלכים, החל מכל ריבוע נתון. מכאן החידה הבאה: -
אם תסתכלו על הריבוע המסומן באותיות, תבינו שיש רק עשרה ריבועים שונים באמת בלוח שחמט - אלה התחומים בקו כהה - כל השאר הם רק היפוכים או שיקופים. לדוגמה, כל A הוא ריבוע פינתי, וכל J הוא ריבוע מרכזי. כתוצאה מכך, מכיוון שלפתרון המוצג יש נקודת מפנה בריבוע D התחום, אנו יכולים לקבל פתרון שמתחיל ומסתיים בכל ריבוע המסומן D - פשוט על ידי סיבוב הלוח. כעת, תוכנית זו תעניק לך סיור שמתחיל מכל A, B, C, D, E, F או H, בעוד שאף מסלול אחר שאני מכיר לא ניתן להתאמה ליותר מחמש נקודות התחלה שונות. אין סיור מלכה בארבעה עשר מהלכים (זכור שסיור חייב להיות חוזר) שיכול להתחיל מ-G, I או J. אבל יכולה להיות לנו דרך לא חוזרת על כל הלוח בארבעה עשר מהלכים, החל מכל ריבוע נתון. מכאן החידה הבאה: - 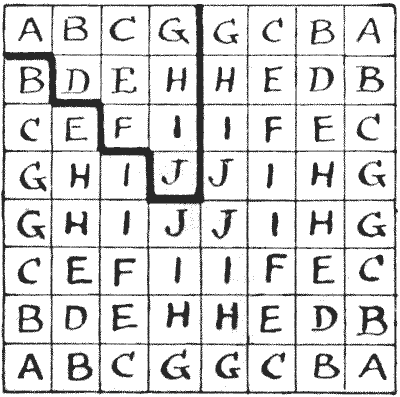 התחל מ-J בחלק הסגור של הדיאגרמה המסומנת באותיות ובקר בכל ריבוע בלוח בארבעה עשר מהלכים, וסיים היכן שתרצה.
התחל מ-J בחלק הסגור של הדיאגרמה המסומנת באותיות ובקר בכל ריבוע בלוח בארבעה עשר מהלכים, וסיים היכן שתרצה.
נושאים:
קומבינטוריקה
->
גאומטריה קומבינטורית
קומבינטוריקה
->
תורת המשחקים
קומבינטוריקה
->
צביעות
->
צביעת שחמט
חידות ורבוסים
- שעשועונים במתמטיקה, הנרי ארנסט דודני שאלה 328
עדיין אין תגובות.