קומבינטוריקה, תורת המשחקים

תורת המשחקים היא חקר קבלת החלטות אסטרטגיות כאשר בחירות של מספר שחקנים מקיימות אינטראקציה. שאלות כוללות ניתוח משחקים (כמו נים, וריאציות של שחמט, או חידות אסטרטגיות) למציאת אסטרטגיות אופטימליות, קביעת מצבי ניצחון/הפסד, או הבנת מושגים כמו שיווי משקל.

  • זאב וכבשים

    המשחק מתבצע על מישור אינסופי. שחקן אחד מזיז את הזאב ושחקן אחר – 50 כבשים. לאחר מהלך של זאב אחת הכבשים עושה מהלך אחר כך שוב זאב וכך הלאה. במהלך אחד הזאב או הכבשה לא הולכים יותר ממטר אחד לכל צד. האם בכל מצב התחלתי הזאב יוכל לתפוס לפחות כבשה אחת? 

    מקורות:

  • משחק עם שוקולד

    יוסי ודני משחקים במשחק הבא. יש להם חפיסת שוקולד בגודל `5xx7` משבצות, שמונחת על שולחן. כל אחד בתורו שובר את אחת מחתיכות השוקולד שיש על השולחן לפי קו ישר ומחזיר את החתיכות שנוצרו לשולחן. כלומר, בתור ראשון שוברים את השוקולד המקורי, ובתורות הבאים בוחרים חתיכה אחת מתוך החתיכות שנוצרו עד אז ושוברים אותה. אפשר לשבור רק לפי קווים של משבצות, וכל שבר הוא מקצה לקצה. מפסיד מי שלא יכול לעשות מהלך. מי שמנצח, אוכל את כל השוקולד.

    מי משניהם יכול להבטיח לעצמו ניצחון, אם יוסי עושה מהלך ראשון?

  • משחק עם ערימות אבנים

    שניים משחקים במשחק הבא. על השולחן נמצאות שלוש ערימות של אבנים. בערימה ראשונה יש `10` אבנים, בשנייה – `15`, בשלישית – `20`. כל אחד בתורו בוחר אחת הערימות שיש כרגע על השולחן ומחלק אותה לשתי ערימות קטנות יותר. מפסיד מי שלא מצליח לעשות מהלך.

    למי משני השחקנים יש אסטרטגיה מנצחת, ומהי?

    מקורות:

  • שאלה

    על השולחן נמצאות 100 כוסות, ובהן `101, 102,...,200` חרצנים. שני אנשים משחקים במשחק הבא: כל אחד בתורו צריך לבחור כוס ולהוציא ממנה מספר כלשהו של חרצנים. אם לאחר מהלך של שחקן מסוים יימצאו שתי כוסות עם מספר זהה של חרצנים, הוא מפסיד. למי יש אסטרטגיית ניצחון: לשחקן הראשון או השני?

    מקורות:

  • סוליטר מרכזי

     

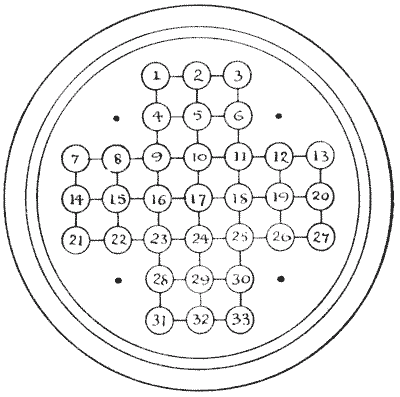
    החידה העתיקה הזו הייתה חביבה מאוד על סבתותינו, ורובנו, אני מתאר לעצמי, נתקלנו מדי פעם בלוח "סוליטר" — לוח עגול מלוטש עם חורים החתוכים בו בדוגמה גיאומטרית, וגולה זכוכית בכל חור. לפעמים שמתי לב לאחד על שולחן צדדי בטרקלין קדמי פרברי, או שמצאתי אחד על מדף בקוטג' כפרי, או ששמו לב לאחד בפונדק דרכים. לפעמים הם מהצורה המוצגת לעיל, אך נפוץ באותה מידה שהלוח יהיו לו ארבעה חורים נוספים, בנקודות המסומנות בנקודות. אני בוחר בצורה הפשוטה יותר.

    אף על פי שלוחי "סוליטר" עדיין נמכרים בחנויות הצעצועים, די יהיה אם הקורא יכין עותק מוגדל של הנ"ל על גיליון קרטון או נייר, ימספר את ה"חורים," ויספק לעצמו `33` אסימונים, כפתורים או שעועית. כעת הניחו אסימון בכל חור פרט למרכזי, מס' `17`, והחידה היא להסיר את כל האסימונים בסדרת קפיצות, למעט האסימון האחרון, שאותו יש להשאיר בחור המרכזי הזה. מותר לך לקפוץ אסימון אחד מעל האסימון הבא לחור פנוי מעבר לו, בדיוק כמו במשחק הדמקה, והאסימון שקפצו מעליו מוסר מיד מהלוח. רק זכור שכל מהלך חייב להיות קפיצה; כתוצאה מכך תסיר אסימון בכל מהלך, ושלושים ואחת קפיצות בודדות כמובן יסירו את כל שלושים ואחד האסימונים. אבל מותרים מהלכים מורכבים (כמו בדמקה, שוב), כל עוד אסימון אחד ממשיך לקפוץ, כל הקפיצות נחשבות למהלך אחד.

    הנה ההתחלה של פתרון דמיוני שישמש כדי להבהיר לחלוטין את אופן התנועה, ולהראות כיצד הפותר צריך לכתוב את ניסיונותיו: `5-17`, `12-10`, `26-12`, `24-26` (`13-11`, `11-25`), `9-11` (`26-24`, `24-10`, `10-12`), וכו', וכו'. הקפיצות הכלולות בסוגריים נחשבות למהלך אחד, מכיוון שהן נעשות עם אותו אסימון. מצא את המספר המועט ביותר של מהלכים אפשריים. כמובן שאסורות קפיצות אלכסוניות; אתה יכול לקפוץ רק בכיוון הקווים.

    מקורות:

  • ביקור אפיסקופלי

    המשבצות הלבנות על לוח השחמט מייצגות את הקהילות של דיוקסיה. הניחו את הרץ על כל משבצת שתרצו, ותכננו כך ש (תוך שימוש בתנועת הרץ הרגילה בשחמט) הוא יבקר בכל אחת מהקהילות שלו במספר המהלכים המועט ביותר האפשרי. כמובן, כל הקהילות שעוברים דרכן בכל מהלך נחשבות כ"ביקורות". אתם יכולים לבקר בכל משבצת יותר מפעם אחת, אך אסור לכם לנוע פעמיים בין אותן שתי משבצות סמוכות. מהו מספר המהלכים המועט ביותר האפשרי? הרץ לא צריך לסיים את ביקורו בקהילה ממנה יצא לדרך לראשונה. מקורות:

  • החידה החדשה של הרץ

     

    זוהי חידה קטנה ומסקרנת למדי. הניחו שמונה רצים (ארבעה שחורים וארבעה לבנים) על לוח השחמט המצומצם, כפי שמוצג באיור. הבעיה היא לגרום לרצים השחורים להחליף מקומות עם הלבנים, כך שאף רץ לא יתקוף רץ אחר מצבע מנוגד. הם חייבים לנוע לחלופין—תחילה רץ לבן, אחר כך רץ שחור, אחר כך רץ לבן, וכן הלאה. כאשר תצליחו לעשות זאת בכלל, נסו למצוא את מספר המהלכים המינימלי האפשרי.

    אם תוציאו את הרצים שעומדים על משבצות שחורות, ותשחקו רק על המשבצות הלבנות, תגלו שהחידה האחרונה שלי הסתובבה על צידה.

    מקורות:

  • סיור המלכה

    החידה של ביצוע סיור שלם בלוח השחמט עם המלכה במספר המהלכים המועט ביותר האפשרי (שבו ניתן לבקר בריבועים יותר מפעם אחת) ניתנה לראשונה על ידי סם לויד המנוח ב-אסטרטגיית שחמט שלו. אבל הפתרון המוצג להלן הוא זה שהוא נתן ב-אגוזי שחמט אמריקאים ב-`1868`. תיעדתי לפחות שישה פתרונות שונים במספר המינימלי של מהלכים - ארבעה עשר - אבל זה הטוב מכולם, מסיבות שאסביר.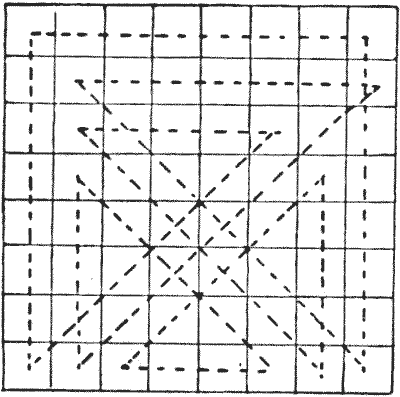 אם תסתכלו על הריבוע המסומן באותיות, תבינו שיש רק עשרה ריבועים שונים באמת בלוח שחמט - אלה התחומים בקו כהה - כל השאר הם רק היפוכים או שיקופים. לדוגמה, כל A הוא ריבוע פינתי, וכל J הוא ריבוע מרכזי. כתוצאה מכך, מכיוון שלפתרון המוצג יש נקודת מפנה בריבוע D התחום, אנו יכולים לקבל פתרון שמתחיל ומסתיים בכל ריבוע המסומן D - פשוט על ידי סיבוב הלוח. כעת, תוכנית זו תעניק לך סיור שמתחיל מכל A, B, C, D, E, F או H, בעוד שאף מסלול אחר שאני מכיר לא ניתן להתאמה ליותר מחמש נקודות התחלה שונות. אין סיור מלכה בארבעה עשר מהלכים (זכור שסיור חייב להיות חוזר) שיכול להתחיל מ-G, I או J. אבל יכולה להיות לנו דרך לא חוזרת על כל הלוח בארבעה עשר מהלכים, החל מכל ריבוע נתון. מכאן החידה הבאה: - 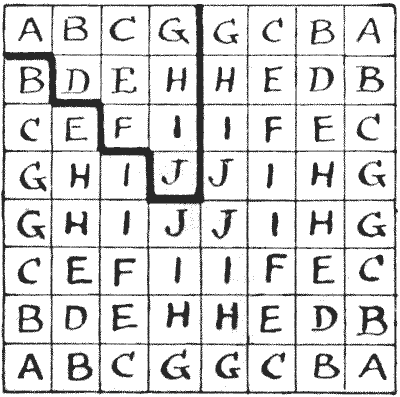התחל מ-J בחלק הסגור של הדיאגרמה המסומנת באותיות ובקר בכל ריבוע בלוח בארבעה עשר מהלכים, וסיים היכן שתרצה. מקורות:

  • הלוח בתאים

     

    איננו יכולים לחלק את לוח השחמט הרגיל לארבעה תאים ריבועיים שווים, ולתאר מסע שלם, או אפילו מסלול, בכל תא. אבל אנחנו יכולים לחלק אותו לארבעה תאים, כפי שמוצג באיור, שניים המכילים כל אחד עשרים משבצות, ושניים האחרים מכילים כל אחד שתים עשרה משבצות, ובכך להשיג חידה מעניינת. אתם מתבקשים לתאר מסע חוזר ונכנס שלם על הלוח הזה, החל מאיפה שתרצו, אך לבקר בכל משבצת בכל תא עוקב לפני שעוברים לתא אחר, ולבצע את הקפיצה הסופית חזרה למשבצת ממנה יצא הפרש. זה לא קשה, אבל יתגלה כמבדר מאוד ולא חסר תועלת.

    האם "מסע" חוזר ונכנס או "נתיב" פרש שלם אפשרי או לא על לוח מלבני ממדים נתונים תלוי לא רק בממדים שלו, אלא גם בצורה שלו. מסע אינו אפשרי באופן ברור על לוח המכיל מספר אי-זוגי של תאים, כגון `5` על `5` או `7` על `7`, מהסיבה הבאה: כל קפיצה עוקבת של הפרש חייבת להיות ממשבצת לבנה לשחורה ושחורה ללבנה לסירוגין. אבל אם יש מספר אי-זוגי של תאים או משבצות חייבת להיות משבצת אחת יותר מצבע אחד מאשר מהצבע השני, לכן הנתיב חייב להתחיל ממשבצת בצבע שנמצא בעודף, ולהסתיים בצבע דומה, ומכיוון שמהלך פרש מצבע אחד לצבע דומה הוא בלתי אפשרי, הנתיב לא יכול להיות חוזר ונכנס. אבל מסע מושלם יכול להתבצע על לוח מלבני בכל מימד, בתנאי שמספר המשבצות יהיה זוגי, ומספר המשבצות בצד אחד לא יהיה קטן מ-`6` ובצד השני לא יהיה קטן מ-`5`. במילים אחרות, הלוח המלבני הקטן ביותר שבו אפשרי מסע חוזר ונכנס הוא לוח בגודל `6` על `5`.

    נתיב פרש שלם (לא חוזר ונכנס) על פני כל המשבצות של לוח לעולם אינו אפשרי אם יש רק שתי משבצות בצד אחד; וגם לא אפשרי על לוח ריבועי ממדים קטנים מ-`5` על `5`. כך שעל לוח `4` על `4` אנחנו לא יכולים לתאר מסע פרש וגם לא נתיב פרש שלם; אנחנו חייבים להשאיר משבצת אחת לא מבוקרת. אבל על לוח `4` על `3` (המכיל ארבע משבצות פחות) ניתן לתאר נתיב שלם בשש עשרה דרכים שונות. זה עשוי לעניין את הקורא לגלות את כולן. כל נתיב שמתחיל ומסתיים במשבצות שונות נספר כאן כפתרון שונה, ואפילו מסלולים הפוכים נקראים שונים.

    מקורות:

  • מסע הפרשייה הקוביסטי

    לפני מספר שנים יצא לי לקרוא איפשהו שאבנית ונדרמונד, מתמטיקאי חכם שנולד ב-`1736` ונפטר ב-`1793`, הקדיש חלק ניכר מזמנו לחקר שאלת מסעי הפרש. מעבר למה שאפשר להבין מכמה אזכורים מקוטעים, אינני מודע לטבע המדויק או לתוצאות מחקריו, אך דבר אחד משך את תשומת ליבי, והייתה זו ההצהרה שהוא הציע את שאלת מסע הפרש על פני שש הפאות של קובייה, כאשר כל פאה היא לוח שחמט. בין אם השיג פתרון ובין אם לא, אינני יודע, אך מעולם לא ראיתי פתרון שפורסם. אז מיד התחלתי לעבוד כדי לשלוט בבעיה מעניינת זו. אולי הקורא ירצה לנסות זאת. מקורות: