DISSECTING A MITRE

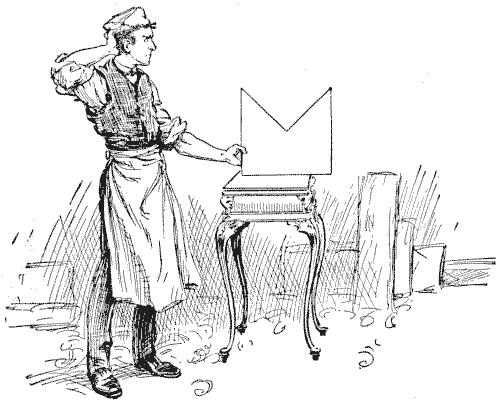
The figure that is perplexing the carpenter in the illustration represents a mitre. It will be seen that its proportions are those of a square with one quarter removed. The puzzle is to cut it into five pieces that will fit together and form a perfect square. I show an attempt, published in America, to perform the feat in four pieces, based on what is known as the "step principle," but it is a fallacy.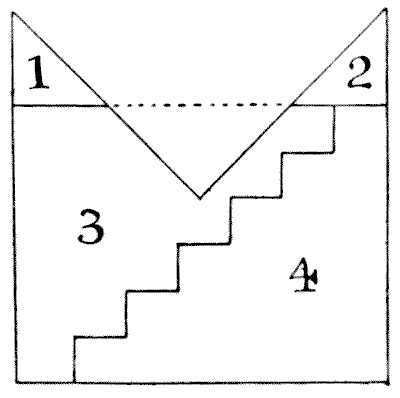  

We are told first to cut oft the pieces `1` and `2` and pack them into the triangular space marked off by the dotted line, and so form a rectangle.

So far, so good. Now, we are directed to apply the old step principle, as shown, and, by moving down the piece `4` one step, form the required square. But, unfortunately, it does not produce a square: only an oblong. Call the three long sides of the mitre `84` in. each. Then, before cutting the steps, our rectangle in three pieces will be `84`×`63`. The steps must be `10`½ in. in height and `12` in. in breadth. Therefore, by moving down a step we reduce by `12` in. the side `84` in. and increase by `10`½ in. the side `63` in. Hence our final rectangle must be `72` in. × `73`½ in., which certainly is not a square! The fact is, the step principle can only be applied to rectangles with sides of particular relative lengths. For example, if the shorter side in this case were `61` `5/7` (instead of `63`), then the step method would apply. For the steps would then be `10` `2/7` in. in height and `12` in. in breadth. Note that `61` `5/7` × `84`= the square of `72`. At present no solution has been found in four pieces, and I do not believe one possible.