几何学, 面积计算

本主题侧重于确定二维表面或区域大小的方法。问题涉及计算各种几何形状（如三角形、四边形、圆形和更复杂的组合图形）的面积，通常需要应用特定的公式。

• 问题

  给定两个边长为 `3` 厘米的正方形。将它们组合在一起形成一个矩形。这个矩形的周长是多少？

  主题：

  算术 几何学 -> 平面几何学 几何学 -> 面积计算 代数学 -> 应用题

• 问题

  萨穆埃尔想要用边长为`25`厘米的正方形瓷砖来铺设一个`3`米乘`4`米的房间。萨穆埃尔需要多少块瓷砖？

  主题：

  算术 几何学 -> 面积计算 代数学 -> 应用题 计量单位

• 问题

  给定凸四边形 ABCD。它的每条边都被分成 K 个相等的部分。边 AB 上的点与 CD 上的对应点相连，BC 上的点与 DA 上的点相连，从而形成 K² 个小四边形。从中选择 K 个四边形，使得每 2 个四边形至少被连接 AB 和 CD 的一条线以及连接 BC 和 DA 的一条线分隔开。证明这些四边形的面积之和为 S_ABCD/K. 
  A. 恩扬斯 

  主题：

  几何学 -> 平面几何学 几何学 -> 面积计算 几何学 -> 向量
  来源：
  • Tournament of Towns, 1979-1980, Main, Spring 问题 5

• 问题

  在一个边长为1的正方形中，画了有限条平行于正方形边的线段，总长度为18（它们可以相交）。证明在正方形被这些线段分割成的所有部分中，至少有一部分的面积不小于0.01。 
  А. Эжанс, А. Берзиньш 

  主题：

  几何学 -> 平面几何学 几何学 -> 面积计算 代数学 -> 不等式 证明与示例 -> 反证法
  来源：
  • Tournament of Towns, 1979-1980, Main, Spring 问题 6

• 问题

  一个有 4k 条边的正多边形被分割成若干个平行四边形。证明在这些平行四边形中，至少有 k 个矩形。求所有矩形的面积之和。

  主题：

  几何学 -> 平面几何学 几何学 -> 面积计算 几何学 -> 立体几何/空间几何 -> 多面体 -> 正多面体

• 问题

  设 ABCD 是一个内接于圆的凸四边形，其对角线互相垂直。O 是圆心。证明折线 AOC 将四边形分成面积相等的两部分。
  沃. 瓦罗瓦金

  主题：

  几何学 -> 面积计算 几何学 -> 平面几何学 -> 圆 几何学 -> 平面几何学 -> 角度计算
  来源：
  • Tournament of Towns, 1980-1981, Spring, Main Version, Grades 9-10 问题 3 积分 5

• 面积与周长

  如果一个正方形的周长增加`10%`，那么它的面积将增加百分之多少？

  主题：

  几何学 -> 面积计算 算术 -> 百分比

• 纸张堆叠

  桌子上有一些相同的矩形纸张。已知最上面的纸张覆盖了任何其他纸张超过一半的面积。是否一定可以在桌子上钉一个钉子，使其穿过所有这些纸张？

  主题：

  组合数学 -> 鸽巢原理 组合数学 -> 组合几何学 几何学 -> 面积计算 几何学 -> 平面几何学 -> 对称性

• 问题

  在一个直角三角形的两个直角边和斜边上构造半圆，如图所示。哪个面积更大 – 是阴影部分的面积还是黑色部分的面积？

  

  主题：

  几何学 -> 面积计算 几何学 -> 平面几何学 -> 三角形 几何学 -> 平面几何学 -> 圆 几何学 -> 平面几何学 -> 勾股定理

• 问题

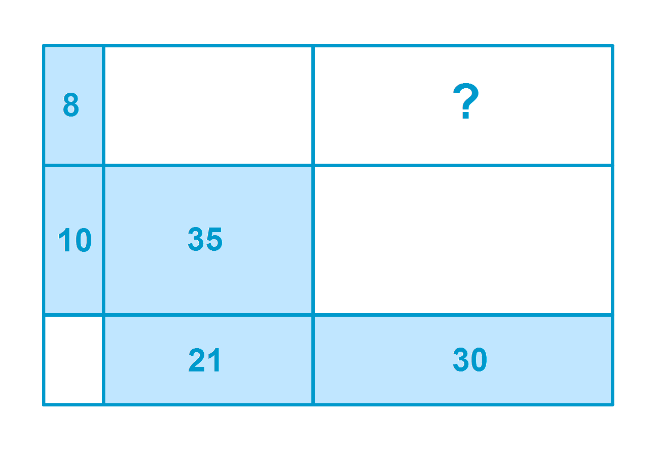
  找出问号标示的区域面积：

  

  主题：

  几何学 -> 平面几何学 几何学 -> 面积计算