חיתוך זוית

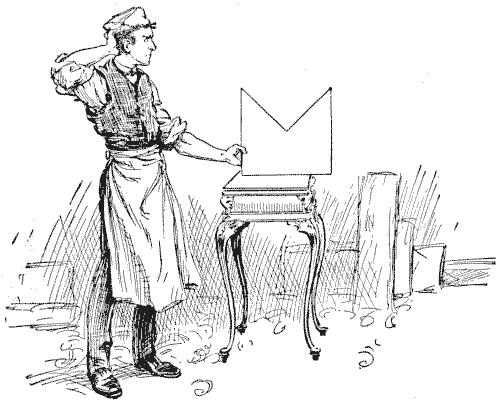
הצורה שמבלבלת את הנגר באיור מייצגת זווית. ניתן לראות שהמידות שלה הן של ריבוע שהוסר ממנו רבע. החידה היא לחתוך אותה לחמישה חלקים שיתאימו זה לזה וייצרו ריבוע מושלם. אני מציג ניסיון, שפורסם באמריקה, לבצע את המשימה בארבעה חלקים, המבוסס על מה שידוע כ"עיקרון הצעד", אבל זו טעות.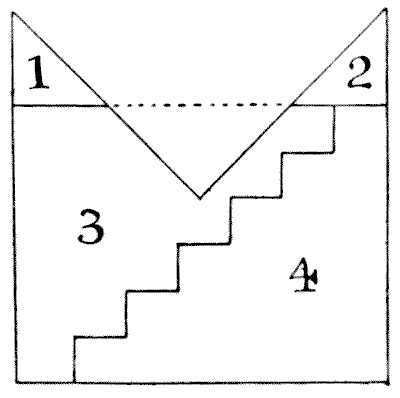  

נאמר לנו תחילה לחתוך את החלקים `1` ו-`2` ולארוז אותם בחלל המשולש המסומן על ידי הקו המקווקו, וכך ליצור מלבן.

עד כאן טוב ויפה. עכשיו, אנו מונחים ליישם את עקרון הצעד הישן, כפי שמוצג, ועל ידי הזזת החלק `4` צעד אחד למטה, ליצור את הריבוע הנדרש. אבל, לצערי, זה לא מייצר ריבוע: רק מלבן. נקרא לשלושת הצדדים הארוכים של הזווית `84` אינץ' כל אחד. אז, לפני חיתוך הצעדים, המלבן שלנו בשלושה חלקים יהיה `84`×`63`. הצעדים צריכים להיות `10`½ אינץ' בגובה ו-`12` אינץ' ברוחב. לכן, על ידי הזזת צעד אחד למטה אנו מקטינים ב-`12` אינץ' את הצד `84` אינץ' ומגדילים ב-`10`½ אינץ' את הצד `63` אינץ'. לכן המלבן הסופי שלנו חייב להיות `72` אינץ' × `73`½ אינץ', מה שבהחלט אינו ריבוע! העובדה היא שניתן ליישם את עקרון הצעד רק על מלבנים עם צלעות באורכים יחסיים מסוימים. לדוגמה, אם הצד הקצר יותר במקרה זה היה `61` `5/7` (במקום `63`), אז שיטת הצעד תתאים. כי אז הצעדים יהיו `10` `2/7` אינץ' בגובה ו-`12` אינץ' ברוחב. שימו לב ש-`61` `5/7` × `84`= הריבוע של `72`. נכון לעכשיו לא נמצא פתרון בארבעה חלקים, ואני לא מאמין שאפשר למצוא כזה.