几何学, 平面几何学
平面几何学关注平面二维表面上的图形和形状。它涵盖点、线、角、多边形(如三角形和四边形)和圆的属性。问题通常涉及与这些元素相关的证明、作图和计算。
面积计算 三角形 圆 对称性 角度计算 勾股定理 三角形不等式-
问题
给定两个边长为 `3` 厘米的正方形。将它们组合在一起形成一个矩形。这个矩形的周长是多少?
-
问题
给定凸四边形 ABCD。它的每条边都被分成 K 个相等的部分。边 AB 上的点与 CD 上的对应点相连,BC 上的点与 DA 上的点相连,从而形成 K2 个小四边形。从中选择 K 个四边形,使得每 2 个四边形至少被连接 AB 和 CD 的一条线以及连接 BC 和 DA 的一条线分隔开。证明这些四边形的面积之和为 SABCD/K.
来源:
A. 恩扬斯 -
问题
在一个边长为1的正方形中,画了有限条平行于正方形边的线段,总长度为18(它们可以相交)。证明在正方形被这些线段分割成的所有部分中,至少有一部分的面积不小于0.01。
来源:
А. Эжанс, А. Берзиньш -
问题
一个有 4k 条边的正多边形被分割成若干个平行四边形。证明在这些平行四边形中,至少有 k 个矩形。求所有矩形的面积之和。
-
问题
游戏在一个无限的平面上进行。一个玩家移动狼,另一个玩家移动 K 只羊。狼走一步后,一只羊走一步,然后狼再走,以此类推。每一步,狼或羊最多只能向任何方向移动一米。在任何初始状态下,狼是否总能抓住至少一只羊?
来源: -
问题
在平面上绘制了一些直线和圆。证明可以将平面划分成的区域涂成两种颜色,使得相邻区域(具有公共线段或弧线)涂成不同的颜色。
-
问题
将给定的形状切割成八个全等的部分:

-
问题
将给定的形状切割成16个全等的部分:
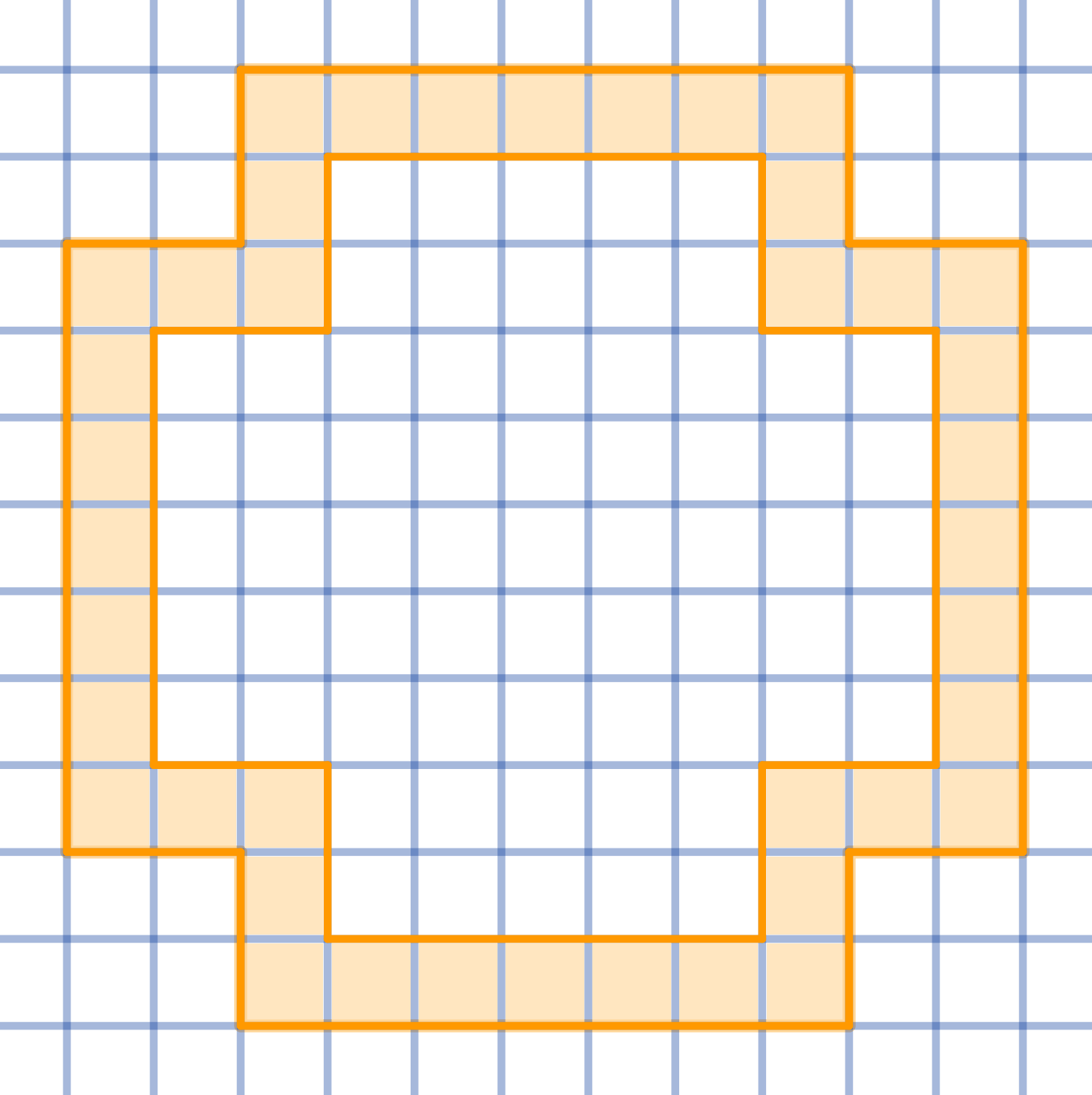
-
问题
找出问号标示的区域面积:
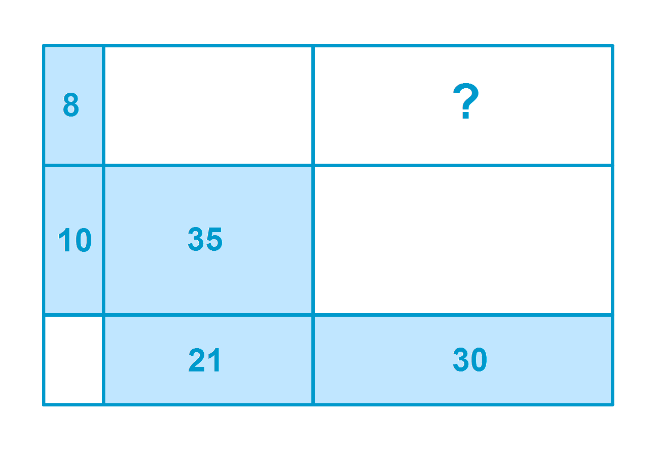
-
问题
给定两个平行四边形:`ABCD` 和 `A^'B^'C^'D^'`。设 `A\A^'` 的中点为 `A^″ `,`B\B^'` 的中点为 `B^″ `,以此类推。证明:`A^″B^″ C^″ D^″ ` 是平行四边形。