Geometry, Plane Geometry, Plane Transformations, Congruence Transformations (Isometries)

Isometries are transformations that preserve distances and angle measures, meaning the transformed figure (image) is congruent to the original figure. These include translations, rotations, and reflections. Questions focus on applying these transformations and understanding their properties.

• Dissect into four parts

  Geometric shapes are called congruent if they coincide when superimposed. Cut the following shape into four congruent parts:

  

  Topics:

  Geometry -> Plane Geometry -> Symmetry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries)
  Sources:
  • Young Mathematician Olympiad, 2019-2020, Final, Grades 3-4 Question 3

• Question

  Given `12` intersecting lines in the plane. Prove that there exist two of these lines such that the angle between them is less than `17^@`.

  Show hint

  Log in here to receive the hint
  Topics:

  Combinatorics -> Pigeonhole Principle Geometry -> Plane Geometry -> Angle Calculation Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries) -> Parallel Translation / Translation

• Triangles on Lines

  Six congruent isosceles triangles are arranged as shown in the figure.
  Show that points C, F, and M are collinear.

  

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Plane Geometry -> Angle Calculation Geometry -> Plane Geometry -> Triangles -> Triangle Congruence Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries) -> Parallel Translation / Translation
  Sources:
  • Gillis Mathematical Olympiad, 2018-2019 Question 3

• Pentagon

  In a convex pentagon `ABCDE`, the following holds: `AE=AD`, `AB=AC`, and `angle CAD=angle ABE + angle AEB`.

  Let `AM` be the median to the side `BE` in the triangle `ABE`. Prove that `AM` is half the length of the segment `CD`.

  Topics:

  Geometry -> Plane Geometry -> Angle Calculation Geometry -> Plane Geometry -> Triangles -> Triangle Congruence Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries) -> Rotation
  Sources:
  • Tournament of Towns, 1983-1984, Fall, Practice Version, Grades 9-10 Question 2 Points 3

• Question

  Inside a square ABCD with side length 1, a point E is marked, and outside the square, a point F is marked, such that triangles ABE and DAF are equilateral. Calculate the area of the pentagon CBEFD.
  

  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Triangles Geometry -> Plane Geometry -> Symmetry Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries) -> Rotation
  Sources:
  • Beno Arbel Olympiad, 2017, Grade 8 Question 6

• CONCERNING WHEELS

   

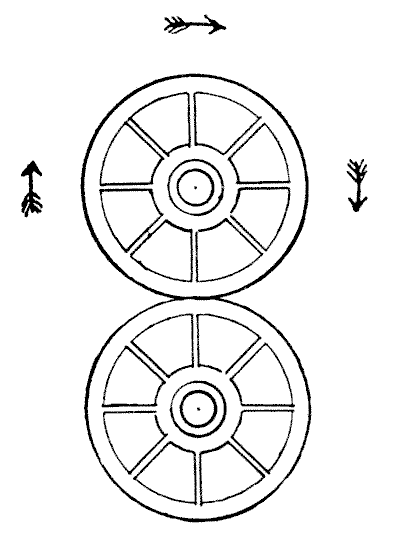
  There are some curious facts concerning the movements of wheels that are apt to perplex the novice. For example: when a railway train is travelling from London to Crewe certain parts of the train at any given moment are actually moving from Crewe towards London. Can you indicate those parts? It seems absurd that parts of the same train can at any time travel in opposite directions, but such is the case.

  In the accompanying illustration we have two wheels. The lower one is supposed to be fixed and the upper one running round it in the direction of the arrows. Now, how many times does the upper wheel turn on its own axis in making a complete revolution of the other wheel? Do not be in a hurry with your answer, or you are almost certain to be wrong. Experiment with two pennies on the table and the correct answer will surprise you, when you succeed in seeing it.

  Topics:

  Geometry -> Plane Geometry -> Circles Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries) -> Rotation
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 203

• Question

  There is a billiard table in the shape of a triangle whose angles are equal to \(90^{\circ}\), \(30^{\circ}\) and \(60^{\circ}\). 

   

  Given a right triangle shaped billiard table, with "pockets" in its corners. One of its acute angles is \(30^{\circ}\). From this corner (the thirty-degree angle) a ball is launched towards the midpoint of the opposite side of the triangle (the median). Prove that if the ball is reflected more than eight times (angle of incidence equals angle of reflection), then eventually the ball will enter the "pocket" located at the 60-degree corner of the triangle.

  Topics:

  Geometry -> Plane Geometry -> Triangles Geometry -> Plane Geometry -> Angle Calculation Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries) -> Reflection

• Question

  Partition the given shape into four congruent parts:

  

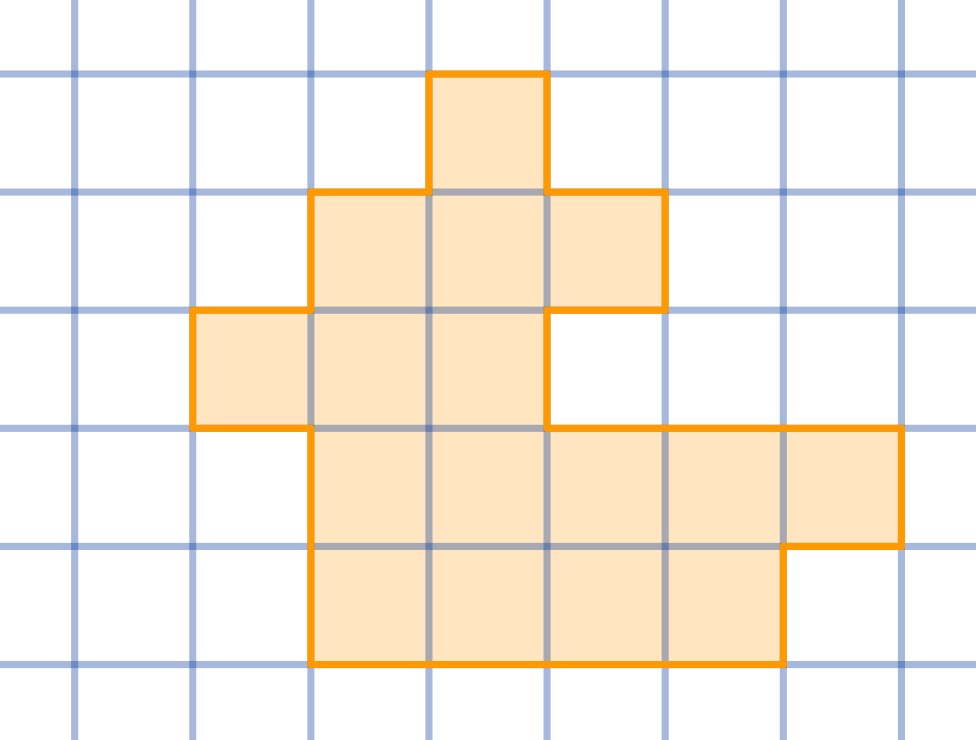  Topics:

  Geometry -> Plane Geometry -> Symmetry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries) -> Reflection

• A Walk in the Plane

  Given a Cartesian coordinate system x-y in the plane. You need to get from the point (1,0) to the point (2006,2005), where in each step you are allowed to move one unit up (in the positive direction of y) or one unit to the right (in the positive direction of the x-axis).

  a. In how many different paths can the task be performed?

  b. In how many different paths can the task be performed if it is forbidden at any stage to pass through a point on the line x=y?

  Topics:

  Combinatorics -> Combinatorial Geometry Combinatorics -> Binomial Coefficients and Pascal's Triangle Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries) -> Reflection
  Sources:
  • Grossman Math Olympiad, 2006 Question 7

• THE MILKMAID PUZZLE

  Here is a little pastoral puzzle that the reader may, at first sight, be led into supposing is very profound, involving deep calculations. He may even say that it is quite impossible to give any answer unless we are told something definite as to the distances. And yet it is really quite "childlike and bland."

   

  In the corner of a field is seen a milkmaid milking a cow, and on the other side of the field is the dairy where the extract has to be deposited. But it has been noticed that the young woman always goes down to the river with her pail before returning to the dairy. Here the suspicious reader will perhaps ask why she pays these visits to the river. I can only reply that it is no business of ours. The alleged milk is entirely for local consumption.

  "Where are you going to, my pretty maid?"
  "Down to the river, sir," she said.
  "I'll not choose your dairy, my pretty maid."
  "Nobody axed you, sir," she said.

  
  If one had any curiosity in the matter, such an independent spirit would entirely disarm one. So we will pass from the point of commercial morality to the subject of the puzzle.

  Draw a line from the milking-stool down to the river and thence to the door of the dairy, which shall indicate the shortest possible route for the milkmaid. That is all. It is quite easy to indicate the exact spot on the bank of the river to which she should direct her steps if she wants as short a walk as possible. Can you find that spot?

  Topics:

  Minimum and Maximum Problems / Optimization Problems Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries) -> Reflection
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 187