Geometry, Plane Geometry, Circles
This topic covers the properties of circles, including radius, diameter, circumference, area, chords, tangents, secants, arcs, and sectors. Questions involve calculations related to these elements and understanding theorems about angles and segments in circles.
Tangent to a Circle-
Question
Let ABCD be a convex quadrilateral inscribed in a circle such that its diagonals are perpendicular to each other. Let O be the center of the circle. Prove that the broken line AOC divides the quadrilateral into two parts of equal area.
V. VarvarkinSources:Topics:Geometry -> Area Calculation Geometry -> Plane Geometry -> Circles Geometry -> Plane Geometry -> Angle Calculation- Tournament of Towns, 1980-1981, Spring, Main Version, Grades 9-10 Question 3 Points 5
-
Question
On a circle, `2016` blue points and one red point are marked. Consider all possible polygons whose vertices are at these points. Which polygons are more numerous – those that contain the red point or those whose vertices are all blue?
Sources: -
Question
Semicircles are constructed on the legs and hypotenuse of a right-angled triangle, as shown in the figure. Which area is largerโthe hatched area or the shaded area?
Topics:Geometry -> Area Calculation Geometry -> Plane Geometry -> Triangles Geometry -> Plane Geometry -> Circles Geometry -> Plane Geometry -> Pythagorean Theorem -
Question
`101` points are located on a circle. Which polygons with vertices at these points are more numerous – polygons with `51` sides or polygons with `50` sides?
-
Question
In the figure, a semicircle is shown with three circles inscribed within it: the large circle, tangent to the diameter of the semicircle at its center, and two smaller circles on the sides, symmetrically arranged. Which area is larger: the shaded area or the unshaded area?
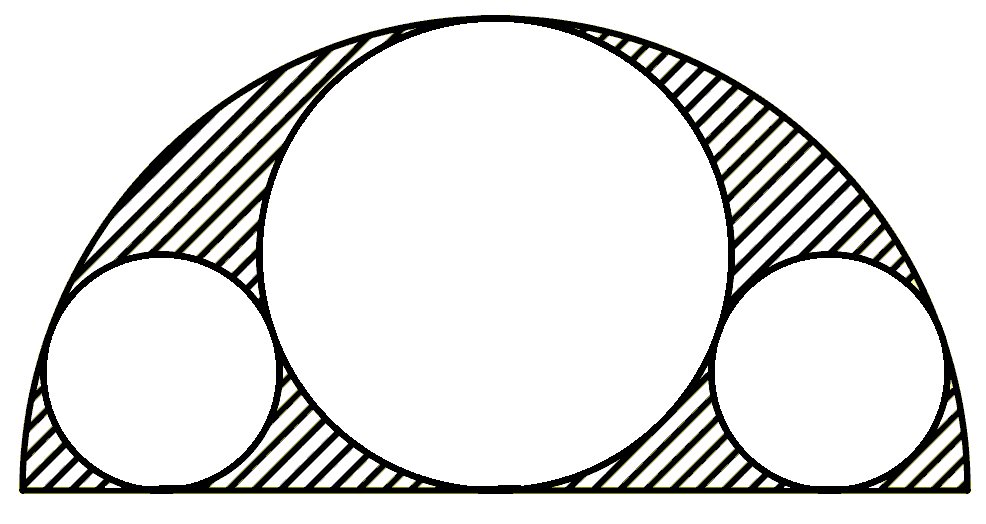Topics:Geometry -> Area Calculation Geometry -> Plane Geometry -> Circles Geometry -> Plane Geometry -> Symmetry -
Quarter Yin-Yang
The shape in the drawing is constructed as follows: Divide the diameter of a semicircle into two equal parts, and construct two additional semicircles on them as diameters: one inwards, and one outwards.
Divide the shape into two congruent parts.
Topics:Geometry -> Area Calculation Geometry -> Plane Geometry -> Circles Geometry -> Plane Geometry -> Symmetry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems -
Question
In a quadrilateral, the lengths of all diagonals and all sides are less than 1. Prove that the quadrilateral can be covered by a circle with a radius of 0.9.
Sources: -
Regular Polygons and Circles
A.
In the right-hand figure, there is a square containing 4 circles. The radii of the circles are equal to each other, and each circle is tangent to two other circles and also to two sides of the square. Find the ratio between the area of the blue part and the area of the white part of the square.
B.
In the left-hand figure, there is a hexagon containing 6 circles with the same radius. Each circle is tangent to two other circles and also to one side of the hexagon, at its midpoint. Find the ratio between the area of the blue part and the area of the white part of the hexagon.
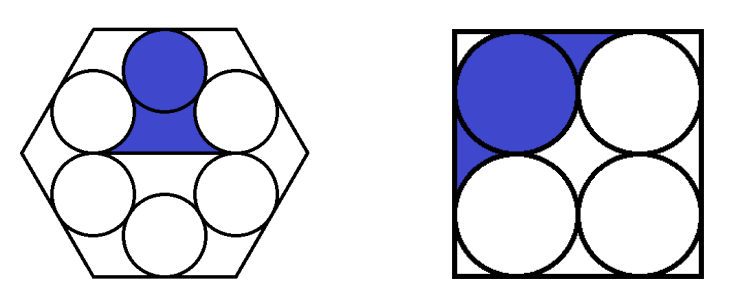
(Solution format: "x, y" for example "1/8, 7/100")
Sources:- Gillis Mathematical Olympiad, 2016-2017 Question 1
-
Area of the Shape
In the image, the area of the semicircle is equal to 1. Find the area of the larger shape, given that all the curved lines in the image are quarter circles.
Sources:
-
Cyclic Quadrilaterals
Given two triangles ACE, BDF
intersecting at 6 points: G,H,I,J,K,L
as shown in the figure. It is given that in each of the quadrilaterals
EFGI, DELH, CDKG, BCJL, ABIK a circle can be inscribed.
Is it possible that a circle can also be inscribed in quadrilateral FAHJ?
Sources:Topics:Geometry -> Solid Geometry / Geometry in Space Geometry -> Plane Geometry -> Circles Algebra -> Equations Algebra -> Inequalities Proof and Example -> Proof by Contradiction Geometry -> Plane Geometry -> Angle Calculation- Gillis Mathematical Olympiad, 2019-2020 Question 5