Geometry, Plane Geometry

Plane Geometry concerns figures and shapes on a flat, two-dimensional surface. It covers properties of points, lines, angles, polygons (like triangles and quadrilaterals), and circles. Questions typically involve proofs, constructions, and calculations related to these elements.

Area Calculation Triangles Circles Symmetry Angle Calculation Pythagorean Theorem Triangle Inequality

• Question

  Given two squares, each with a side length of `3` centimeters, and joined together to form a rectangle, what is the perimeter of the resulting rectangle?

  Topics:

  Arithmetic Geometry -> Plane Geometry Geometry -> Area Calculation Algebra -> Word Problems

• Question

  Given a convex quadrilateral ABCD. Each of its sides is divided into K equal parts. Points on side AB are connected to corresponding points on CD, and points on BC are connected to points on DA, creating K² smaller quadrilaterals. From these, K quadrilaterals are chosen such that any two quadrilaterals are separated by at least one line connecting AB and CD, and one line connecting BC and DA. Prove that the sum of the areas of these quadrilaterals is S_ABCD/K. 
  By A. Angans. 

  Topics:

  Geometry -> Plane Geometry Geometry -> Area Calculation Geometry -> Vectors
  Sources:
  • Tournament of Towns, 1979-1980, Main, Spring Question 5

• Question

  In a square with side length 1, a finite number of segments parallel to the sides of the square were drawn, with a total length of 18 (they can intersect). Prove that among the parts into which the square is divided by the segments, there is a part with an area of at least 0.01. 
  A. Engenes, A. Brazins 

  Topics:

  Geometry -> Plane Geometry Geometry -> Area Calculation Algebra -> Inequalities Proof and Example -> Proof by Contradiction
  Sources:
  • Tournament of Towns, 1979-1980, Main, Spring Question 6

• Question

  A regular polygon with 4k sides is divided into parallelograms. Prove that among these parallelograms there are at least k rectangles. Find the sum of the areas of all the rectangles.

  Topics:

  Geometry -> Plane Geometry Geometry -> Area Calculation Geometry -> Solid Geometry / Geometry in Space -> Polyhedra -> Regular Polyhedra

• Question

  The game takes place on an infinite plane. One player moves the wolf, and another player moves K sheep. After the wolf's move, one of the sheep makes a move, then the wolf again, and so on. In one move, the wolf or a sheep cannot move more than one meter in any direction. Can the wolf always catch at least one sheep, regardless of the initial positions?

  Topics:

  Combinatorics -> Combinatorial Geometry Combinatorics -> Invariants Geometry -> Plane Geometry Logic -> Reasoning / Logic Proof and Example -> Constructing an Example / Counterexample Minimum and Maximum Problems / Optimization Problems
  Sources:
  • Tournament of Towns, 1980-1981, Spring, Main Version, Grades 11-12 Question 2

• Question

  A number of lines and circles are drawn in the plane. Prove that it is possible to color the regions into which the plane is divided using two colors such that neighboring regions (those sharing a line segment or arc) are colored with different colors.

  Topics:

  Combinatorics -> Combinatorial Geometry Combinatorics -> Induction (Mathematical Induction) Geometry -> Plane Geometry Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Colorings

• Question

  Cut the given shape into eight congruent parts:

  

  Topics:

  Geometry -> Plane Geometry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry

• Question

  Divide the given shape into 16 congruent parts:

  

  Topics:

  Geometry -> Plane Geometry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry

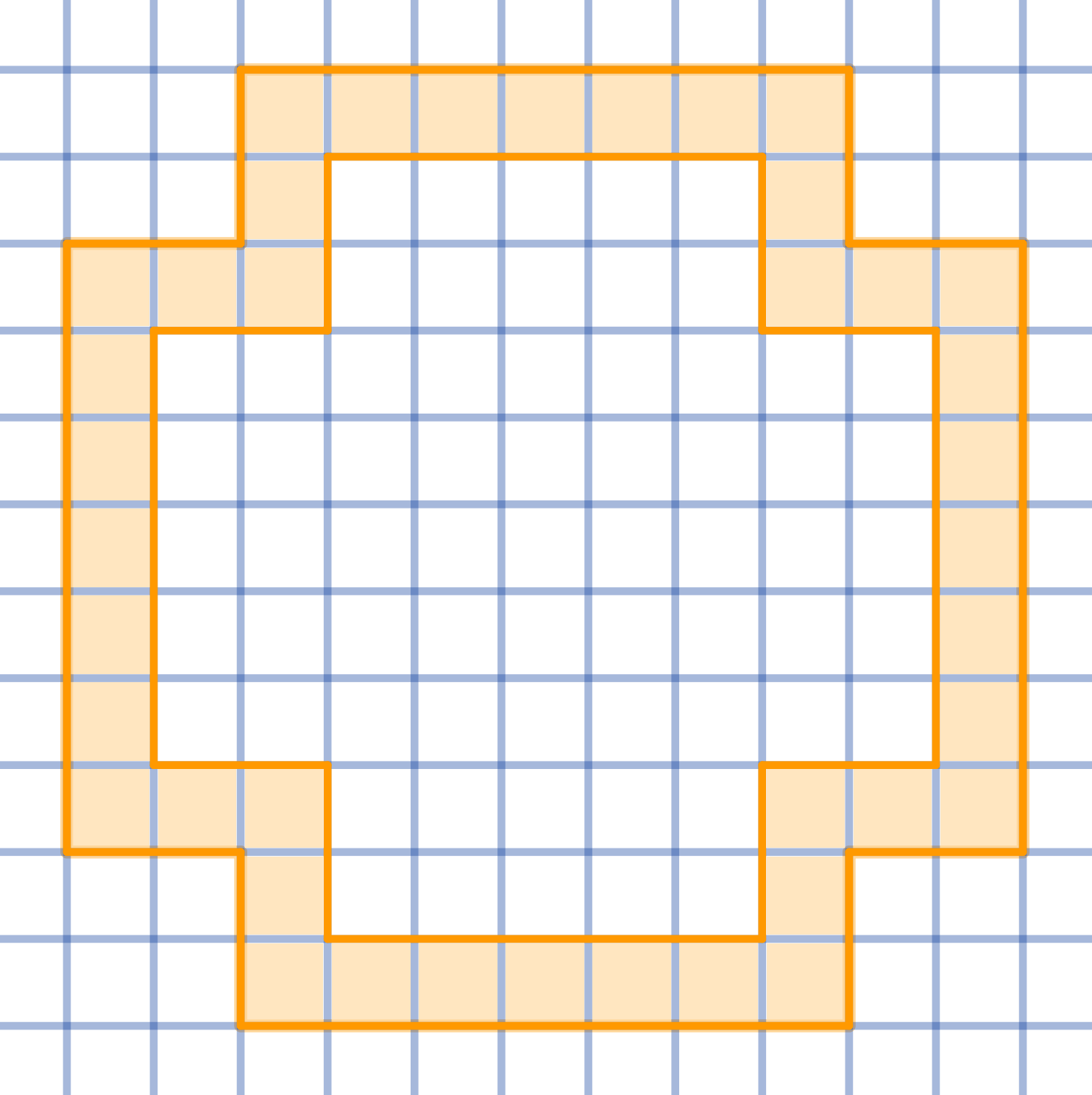
• Question

  Find the area marked by the question mark:

  

  Topics:

  Geometry -> Plane Geometry Geometry -> Area Calculation

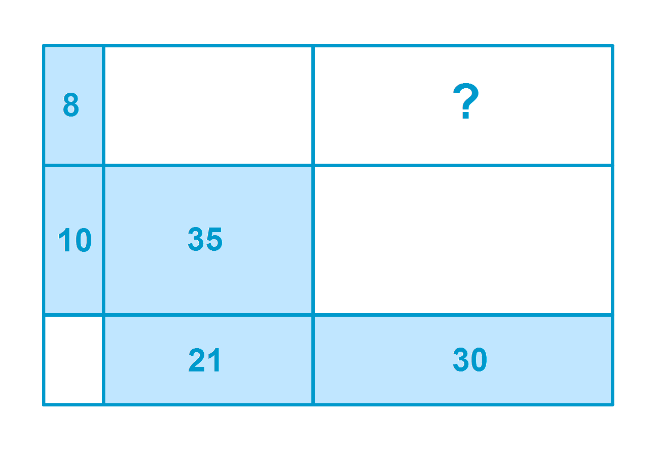
• Question

  Given two parallelograms: `ABCD` and `A^'B^'C^'D^'`. Let `A^″ ` be the midpoint of the segment `A\A^'`, `B^″ ` be the midpoint of the segment `B\B^'`, and so on. Prove that `A^″B^″ C^″ D^″ ` is a parallelogram.

  Topics:

  Geometry -> Plane Geometry Geometry -> Vectors