Geometry, Plane Geometry, Triangles

This subject explores the properties, types (e.g., equilateral, isosceles, scalene, right-angled), and theorems related to triangles, which are fundamental three-sided polygons. Questions often involve calculating angles, side lengths, area, perimeter, and applying triangle-specific theorems.

• Question

  There is a billiard table in the shape of a triangle whose angles are equal to \(90^{\circ}\), \(30^{\circ}\) and \(60^{\circ}\). 

   

  Given a right triangle shaped billiard table, with "pockets" in its corners. One of its acute angles is \(30^{\circ}\). From this corner (the thirty-degree angle) a ball is launched towards the midpoint of the opposite side of the triangle (the median). Prove that if the ball is reflected more than eight times (angle of incidence equals angle of reflection), then eventually the ball will enter the "pocket" located at the 60-degree corner of the triangle.

  Topics:

  Geometry -> Plane Geometry -> Triangles Geometry -> Plane Geometry -> Angle Calculation Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries) -> Reflection

• Question

  In the plane, a square and a point `P` are given. Prove that it is impossible for the distances from `P` to the vertices of the square to be `1`, `1`, `2`, and `3` centimeters?

  Topics:

  Geometry -> Plane Geometry -> Triangles Proof and Example -> Proof by Contradiction Geometry -> Plane Geometry -> Triangle Inequality

• Question

  Semicircles are constructed on the legs and hypotenuse of a right-angled triangle, as shown in the figure. Which area is larger—the hatched area or the shaded area?

  

  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Triangles Geometry -> Plane Geometry -> Circles Geometry -> Plane Geometry -> Pythagorean Theorem

• Question

  A square is divided into several convex polygons (more than `1`), each of which has a different number of sides. Prove that among these polygons there is a triangle.

  Topics:

  Combinatorics -> Pigeonhole Principle Combinatorics -> Combinatorial Geometry Combinatorics -> Graph Theory Geometry -> Plane Geometry -> Triangles Proof and Example -> Proof by Contradiction Geometry -> Solid Geometry / Geometry in Space -> Polyhedra Minimum and Maximum Problems / Optimization Problems

• Question

  Is it possible to cut a triangle into four convex shapes: a triangle, a quadrilateral, a pentagon, and a hexagon?

  Topics:

  Geometry -> Plane Geometry -> Triangles Proof and Example -> Constructing an Example / Counterexample Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems

• Question

  How many triangles are there in the image?

  

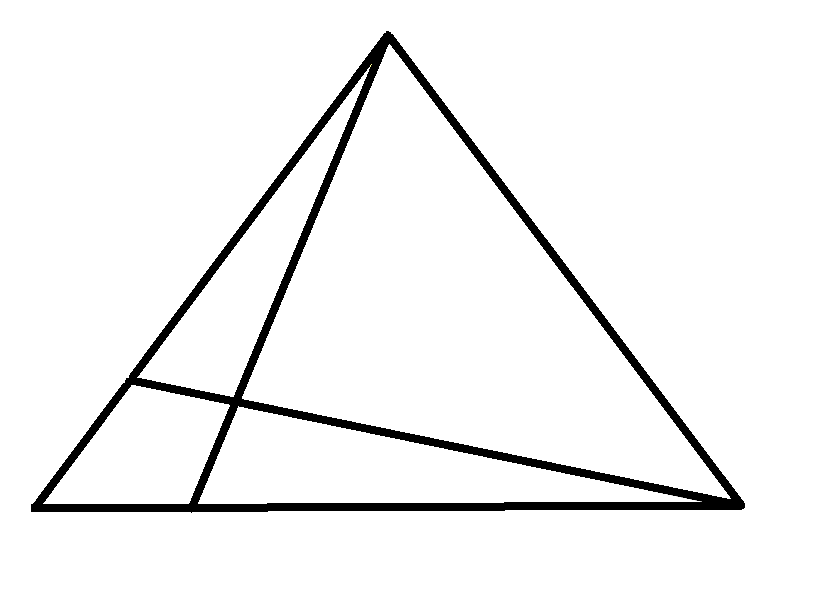  Topics:

  Geometry -> Plane Geometry -> Triangles Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures

• Question

  A plane is colored with two colors (that is, every point on the plane is colored with one of these two colors). Prove that there exist two points on the plane at a distance of `1` such that they are both the same color.

  Topics:

  Combinatorics -> Pigeonhole Principle Combinatorics -> Combinatorial Geometry Geometry -> Plane Geometry -> Triangles Proof and Example -> Constructing an Example / Counterexample Proof and Example -> Proof by Contradiction

• Question

  Let the sides of a triangle be a, b, c and the lengths of the corresponding medians be `m_a , m_b, m_c`. Show that

  `sum_{cyc} m_a / a >= {3( m_a + m_b + m_c)} /{a + b + c}`

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Plane Geometry -> Triangles Algebra -> Inequalities Geometry -> Plane Geometry -> Triangle Inequality
  Sources:
  • Mink Exercises and Additional Competition Materials, 2018-2019, Exercise 1

• Triangles in a Hexagon

  How many triangles are in the picture? Count all the triangles formed by the lines.

  

  Show hint

  Log in here to receive the hint
  Topics:

  Combinatorics Geometry -> Plane Geometry -> Triangles
  Sources:
  • Young Mathematician Olympiad, 2017-2018, Stage A, Grades 3-4 Question 3

• Product of Areas

  In the diagram, there is a quadrilateral with perpendicular diagonals. Prove that the product of the areas of the shaded regions within the quadrilateral is equal to the product of the areas of the unshaded regions within the quadrilateral.

  

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Triangles
  Sources:
  • Young Mathematician Olympiad, 2017-2018, Final, Grades 5-6 Question 3