Combinatorics, Binomial Coefficients and Pascal's Triangle

Binomial coefficients, denoted `\binom{n}{k}`, count the number of ways to choose `k` items from a set of `n` items. Pascal's Triangle is a triangular array of these coefficients with many interesting properties. Questions involve calculating coefficients, applying binomial theorem, and using properties of Pascal's Triangle.

• Question

  `101` points are located on a circle. Which polygons with vertices at these points are more numerous – polygons with `51` sides or polygons with `50` sides?

  Topics:

  Combinatorics -> Binomial Coefficients and Pascal's Triangle Combinatorics -> Matchings Geometry -> Plane Geometry -> Circles

• Question

  A cannibal captured `6` people.

  a. In how many different ways can he choose one person for breakfast, one person for lunch, and one person for dinner?

  b. In how many different ways can he choose three people to release them?

  Topics:

  Combinatorics -> Binomial Coefficients and Pascal's Triangle Combinatorics -> Product Rule / Rule of Product Number Theory -> Division

• Question

  A wizard summoned `20` knights, of which `10` were elves and `10` were dwarves. The wizard wants to choose a team from them to perform a secret mission. This team must contain equal numbers of elves and dwarves.

  How many possibilities are there for such a team? (Note that he cannot choose an empty team)

  Show hint

  Log in here to receive the hint
  Topics:

  Combinatorics -> Binomial Coefficients and Pascal's Triangle Set Theory

• A Walk in the Plane

  Given a Cartesian coordinate system x-y in the plane. You need to get from the point (1,0) to the point (2006,2005), where in each step you are allowed to move one unit up (in the positive direction of y) or one unit to the right (in the positive direction of the x-axis).

  a. In how many different paths can the task be performed?

  b. In how many different paths can the task be performed if it is forbidden at any stage to pass through a point on the line x=y?

  Topics:

  Combinatorics -> Combinatorial Geometry Combinatorics -> Binomial Coefficients and Pascal's Triangle Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries) -> Reflection
  Sources:
  • Grossman Math Olympiad, 2006 Question 7

• A BANK HOLIDAY PUZZLE

  Two friends were spending their bank holiday on a cycling trip. Stopping for a rest at a village inn, they consulted a route map, which is represented in our illustration in an exceedingly simplified form, for the puzzle is interesting enough without all the original complexities. They started from the town in the top left-hand corner marked A. It will be seen that there are one hundred and twenty such towns, all connected by straight roads. Now they discovered that there are exactly `1,365` different routes by which they may reach their destination, always travelling either due south or due east. The puzzle is to discover which town is their destination.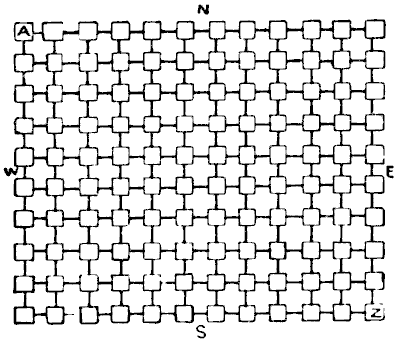 Of course, if you find that there are more than `1,365` different routes to a town it cannot be the right one.
  Topics:

  Combinatorics -> Binomial Coefficients and Pascal's Triangle
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 253