Number Theory, Prime Numbers

Prime numbers are natural numbers greater than 1 that have no positive divisors other than 1 and themselves. This topic explores their properties, identification, distribution (e.g., Sieve of Eratosthenes), and their fundamental role in number theory (e.g., prime factorization).

• The Number

  Given a positive integer less than 2000.
  If it is not divisible by 43, then it is divisible by 41,
  If it is not divisible by 53, then it is divisible by 43,
  If it is not divisible by 41, then it is divisible by 53.
  Find the number.

  Topics:

  Number Theory -> Prime Numbers Arithmetic Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules Logic -> Reasoning / Logic Number Theory -> Greatest Common Divisor (GCD) and Least Common Multiple (LCM) Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Number Theory -> Division
  Sources:
  • Young Mathematician Olympiad, 2019-2020, Stage B, Grades 3-4 Question 6
  • Young Mathematician Olympiad, 2019-2020, Stage B, Grades 5-6 Question 4

• THE BANKER'S PUZZLE

  A banker had a sporting customer who was always anxious to wager on anything. Hoping to cure him of his bad habit, he proposed as a wager that the customer would not be able to divide up the contents of a box containing only sixpences into an exact number of equal piles of sixpences. The banker was first to put in one or more sixpences (as many as he liked); then the customer was to put in one or more (but in his case not more than a pound in value), neither knowing what the other put in. Lastly, the customer was to transfer from the banker's counter to the box as many sixpences as the banker desired him to put in. The puzzle is to find how many sixpences the banker should first put in and how many he should ask the customer to transfer, so that he may have the best chance of winning.
  Topics:

  Number Theory -> Prime Numbers Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Euler's Theorem and Fermat's Little Theorem
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 134

• THE DUTCHMEN'S WIVES

  I wonder how many of my readers are acquainted with the puzzle of the "Dutchmen's Wives"—in which you have to determine the names of three men's wives, or, rather, which wife belongs to each husband. Some thirty years ago it was "going the rounds," as something quite new, but I recently discovered it in the Ladies' Diary for `1739-40`, so it was clearly familiar to the fair sex over one hundred and seventy years ago. How many of our mothers, wives, sisters, daughters, and aunts could solve the puzzle to-day? A far greater proportion than then, let us hope.

  Three Dutchmen, named Hendrick, Elas, and Cornelius, and their wives, Gurtrün, Katrün, and Anna, purchase hogs. Each buys as many as he (or she) gives shillings for one. Each husband pays altogether three guineas more than his wife. Hendrick buys twenty-three more hogs than Katrün, and Elas eleven more than Gurtrün. Now, what was the name of each man's wife?

  Topics:

  Number Theory -> Prime Numbers Arithmetic Algebra -> Word Problems Algebra -> Equations -> Diophantine Equations
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 139

• MAGIC SQUARES OF TWO DEGREES

  While reading a French mathematical work I happened to come across, the following statement: "A very remarkable magic square of `8`, in two degrees, has been constructed by M. Pfeffermann. In other words, he has managed to dispose the sixty-four first numbers on the squares of a chessboard in such a way that the sum of the numbers in every line, every column, and in each of the two diagonals, shall be the same; and more, that if one substitutes for all the numbers their squares, the square still remains magic." I at once set to work to solve this problem, and, although it proved a very hard nut, one was rewarded by the discovery of some curious and beautiful laws that govern it. The reader may like to try his hand at the puzzle.

  Topics:

  Number Theory -> Prime Numbers Combinatorics -> Number Tables
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 408

• THE BASKETS OF PLUMS

   

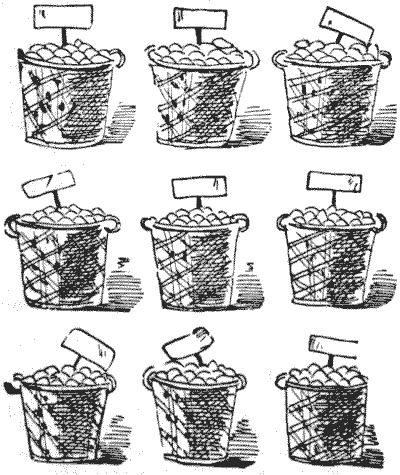
  This is the form in which I first introduced the question of magic squares with prime numbers. I will here warn the reader that there is a little trap.

  A fruit merchant had nine baskets. Every basket contained plums (all sound and ripe), and the number in every basket was different. When placed as shown in the illustration they formed a magic square, so that if he took any three baskets in a line in the eight possible directions there would always be the same number of plums. This part of the puzzle is easy enough to understand. But what follows seems at first sight a little queer.

  The merchant told one of his men to distribute the contents of any basket he chose among some children, giving plums to every child so that each should receive an equal number. But the man found it quite impossible, no matter which basket he selected and no matter how many children he included in the treat. Show, by giving contents of the nine baskets, how this could come about.

  Topics:

  Number Theory -> Prime Numbers Combinatorics
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 409

• THE MANDARIN'S "T" PUZZLE

   

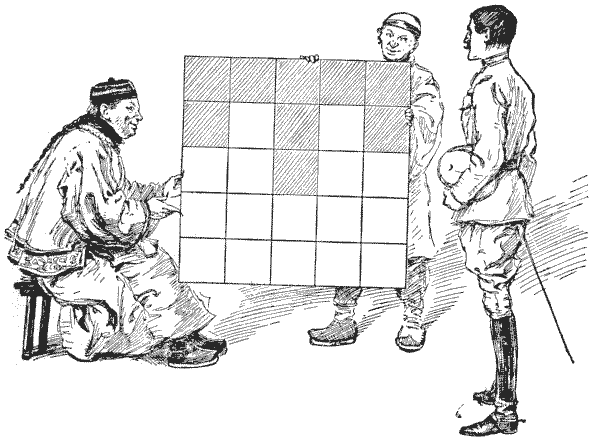
  Before Mr. Beauchamp Cholmondely Marjoribanks set out on his tour in the Far East, he prided himself on his knowledge of magic squares, a subject that he had made his special hobby; but he soon discovered that he had never really touched more than the fringe of the subject, and that the wily Chinee could beat him easily. I present a little problem that one learned mandarin propounded to our traveller, as depicted on the last page.

  The Chinaman, after remarking that the construction of the ordinary magic square of twenty-five cells is "too velly muchee easy," asked our countryman so to place the numbers `1` to `25` in the square that every column, every row, and each of the two diagonals should add up `65`, with only prime numbers on the shaded "T." Of course the prime numbers available are `1, 2, 3, 5, 7, 11, 13, 17, 19`, and `23`, so you are at liberty to select any nine of these that will serve your purpose. Can you construct this curious little magic square?

  Topics:

  Number Theory -> Prime Numbers Arithmetic Combinatorics Logic Puzzles and Rebuses
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 410

• A MAGIC SQUARE OF COMPOSITES

  As we have just discussed the construction of magic squares with prime numbers, the following forms an interesting companion problem. Make a magic square with nine consecutive composite numbers—the smallest possible.
  Topics:

  Number Theory -> Prime Numbers
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 411

• Question

  Find all integer solutions `(k>1) y^k=x^2+x`

  Topics:

  Number Theory -> Prime Numbers -> Prime Factorization Number Theory -> Greatest Common Divisor (GCD) and Least Common Multiple (LCM) Algebra -> Equations -> Diophantine Equations
  Sources:
  • Tournament of Towns, 1980-1981, Spring, Main Version, Grades 9-10 Question 1 Points 3

• Question

  Find five natural numbers whose sum is `20`, and whose product is `420`.

  Topics:

  Number Theory -> Division -> Parity (Even/Odd) Proof and Example -> Constructing an Example / Counterexample Number Theory -> Prime Numbers -> Prime Factorization
  Sources:
  • problems.ru web site

• Question

  Represent the number `203` as the product of several natural numbers different from `203`, such that the sum of these numbers is also equal to `203`.

  Show hint

  Log in here to receive the hint
  Topics:

  Number Theory -> Prime Numbers -> Prime Factorization
  Sources:
  • problems.ru web site