Combinatorics, Number Tables

Problems in this category involve grids or tables filled with numbers. Tasks might include finding patterns, determining missing entries based on a rule, calculating sums of rows/columns/diagonals, or analyzing properties of specific arrangements like magic squares.

• Three Friends

  There are three friends, Weiss, Schwartzman, and Rotenberg. This trio of friends is special because one of them is blonde, one is ginger (redhead), and one has black hair. One day, the blonde guy said to Schwartzman: "We are a very special trio of friends! Notice that it's not only that the last names of the three of us mean colors, but also that each of our last names does not match his hair color."

  What hair color does each of these three people have?

  Note: "Schwartzman" means "black man", "Rotenberg" means "red mountain" and "Weiss" means "white" (from Yiddish).

  Topics:

  Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Number Tables Logic -> Truth-tellers and Liars Problems
  Sources:
  • problems.ru web site

• Question

  A `29×29` table contains all integers from `1` to `29`, each appearing exactly `29` times. The sum of all numbers above the main diagonal is exactly three times greater than the sum of all numbers below the main diagonal. What number is written in the central cell of the table?

  Topics:

  Arithmetic Logic -> Reasoning / Logic Algebra -> Sequences Algebra -> Inequalities -> Averages / Means Combinatorics -> Number Tables Minimum and Maximum Problems / Optimization Problems

• Differences in the Multiplication Table

  Color the `10xx10` multiplication table with a black and white chessboard coloring, such that the cell of `1xx1` is colored black.
  Find the difference between the sum of all the numbers in the black cells and the sum of all the numbers in the white cells.
   

  	1	2	3	4	5	6	7	8	9	10
  1	1	2	3	4	5	6	7	8	9	10
  2	2	4	6	8	10	12	14	16	18	20
  3	3	6	9	12	15	18	21	24	27	30
  4	4	8	12	16	20	24	28	32	36	40
  5	5	10	15	20	25	30	35	40	45	50
  6	6	12	18	24	30	36	42	48	54	60
  7	7	14	21	28	35	42	49	56	63	70
  8	8	16	24	32	40	48	56	64	72	80
  9	9	18	27	36	45	54	63	72	81	90
  10	10	20	30	40	50	60	70	80	90	100

  Show hint

  Log in here to receive the hint
  Topics:

  Arithmetic Combinatorics -> Number Tables Combinatorics -> Colorings -> Chessboard Coloring
  Sources:
  • Young Mathematician Olympiad, 2017-2018, Stage A, Grades 3-4 Question 8
  • Young Mathematician Olympiad, 2017-2018, Stage A, Grades 5-6 Question 8

• What is in each container?

  On the table, a cup, glass, pitcher, and jar are arranged in a row in an unknown order. The containers hold milk, orange juice, cola, and water, but it is unknown which liquid is in each container. Given that:

  • The milk and water are not in the cup.
  • The container holding orange juice is between the pitcher and the container holding cola.
  • The jar does not contain water or orange juice.
  • The glass is between the jar and the container with the milk.

  Which liquid is in which container?

   

  Show hint

  Log in here to receive the hint
  Topics:

  Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Number Tables

• Sum of Products of Digits

  Let `P(n)` denote the product of the digits of the number `n`. For example, `P(1948) = 1 * 9 * 4 * 8 = 288`.

  A.

  Calculate `P(1) + P(2) + P(3) + ... + P(2016)`

  B.

  Find the maximum value of `{P(n)} /n`, where `2016 <= n <= 5777`.

  (Solution format: "x, y/z" where y/z is an unreduced fraction. For example "10000, 35/100")

  Show hint

  Log in here to receive the hint
  Topics:

  Arithmetic Algebra -> Word Problems Combinatorics -> Number Tables Number Theory -> Division
  Sources:
  • Gillis Mathematical Olympiad, 2016-2017 Question 2

• A 2022x2022 Board and Inversion Operations

  We have a `2022 times 2022` board with real numbers.

  In each move, we can choose a row or a column and a real number `c`.

  Then, we replace each number in the row or column from `x` to `c - x`.

  Is it possible to get from any board to any other board?

   

  Show hint

  Log in here to receive the hint
  Topics:

  Combinatorics -> Invariants Algebra Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Number Tables

• Minimal Table

  Given a table of size `3 times 3`. Hilla wants to write digits from 1 to 9 in the table's cells, such that all the sums in the rows and columns of the table are different, and the total sum of the table is as small as possible.
  It is allowed to repeat the same digit multiple times. What is the smallest sum that Hilla can obtain?

  Topics:

  Arithmetic Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Number Tables
  Sources:
  • Young Mathematician Olympiad, 2018-2019, Stage B, Grades 5-6 Question 7

• The missing number

  Find a number such that if we write it in each of the blue squares, the sums in all `3times3` squares in the table will be equal to each other.

  

  Topics:

  Combinatorics -> Number Tables
  Sources:
  • Young Mathematician Olympiad, 2020-2021, Stage A, Grades 3-4 Question 1

• THE VOTERS' PUZZLE

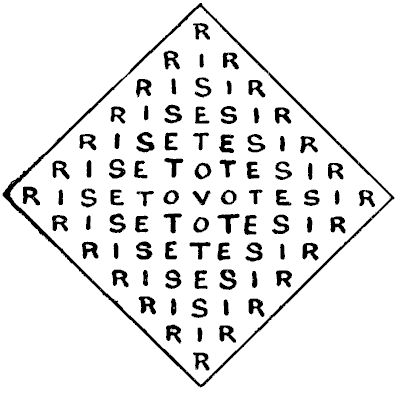  Here we have, perhaps, the most interesting form of the puzzle. In how many different ways can you read the political injunction, "RISE TO VOTE, SIR," under the same conditions as before? In this case every reading of the palindrome requires the use of the central V as the middle letter.
  Topics:

  Combinatorics -> Number Tables
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 258

• COUNTER CROSSES

  All that we need for this puzzle is nine counters, numbered `1, 2, 3, 4, 5, 6, 7, 8`, and `9`. It will be seen that in the illustration A these are arranged so as to form a Greek cross, while in the case of B they form a Latin cross. In both cases the reader will find that the sum of the numbers in the upright of the cross is the same as the sum of the numbers in the horizontal arm. It is quite easy to hit on such an arrangement by trial, but the problem is to discover in exactly how many different ways it may be done in each case. Remember that reversals and reflections do not count as different. That is to say, if you turn this page round you get four arrangements of the Greek cross, and if you turn it round again in front of a mirror you will get four more. But these eight are all regarded as one and the same. Now, how many different ways are there in each case?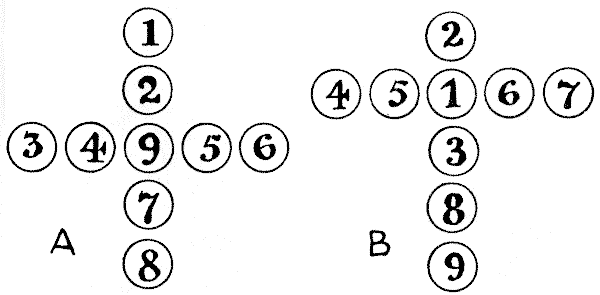
  Topics:

  Combinatorics -> Product Rule / Rule of Product Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Number Tables
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 277