Combinatorics, Product Rule / Rule of Product

The Rule of Product is a fundamental counting principle: if there are `n` ways to do one task and `m` ways to do another task, then there are `n \times m` ways to perform both tasks. Questions involve applying this rule to count sequences of choices or outcomes.

• Question

  In a `3×3` table, each of the squares can be colored black, or it can be left white. How many such colorings are there?

  Show hint

  Log in here to receive the hint
  Topics:

  Combinatorics -> Product Rule / Rule of Product

• Question

  In the "Sport-Toto" lottery, one must predict the results of soccer games – in each game, a win for the first team, a win for the second team, or a draw, without regard to the exact score. How many different ways are there to fill out a lottery ticket if each ticket contains `13` different games?

  Show hint

  Log in here to receive the hint
  Topics:

  Combinatorics -> Product Rule / Rule of Product

• Question

  In a company, there are `13` people, including the manager. One day, the manager decided to appoint a deputy, an alternate, a secretary, and a clerk from the company's employees. In how many different ways can he do this, if the skills of the employees do not affect the type of positions they can fill?

  Topics:

  Combinatorics -> Product Rule / Rule of Product

• Question

  A cannibal captured `6` people.

  a. In how many different ways can he choose one person for breakfast, one person for lunch, and one person for dinner?

  b. In how many different ways can he choose three people to release them?

  Topics:

  Combinatorics -> Binomial Coefficients and Pascal's Triangle Combinatorics -> Product Rule / Rule of Product Number Theory -> Division

• Question

  In a class of `30` students, each one is allowed to go on the annual trip or stay at home. What is the number of possible combinations for going on the trip?

  Topics:

  Combinatorics -> Product Rule / Rule of Product

• Divisible by 2 or 5 but not 3

  How many five-digit numbers are divisible by 2 or 5, but not divisible by 3?

  Topics:

  Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules -> Divisibility Rules by 3 and 9 Combinatorics -> Product Rule / Rule of Product
  Sources:
  • Young Mathematician Olympiad, 2018-2019, Stage B, Grades 5-6 Question 4

• More Numbers with Ascending Digits

  Miri writes down all the numbers whose decimal representation contains only the digits `1, 2, 3, 4, 5, 6`.
  (Not all digits must appear) and all the digits that appear are written in ascending order (e.g., 1356 or 124 or 5 but not 162 and not 1223).
  How many numbers will Miri write down?

  Topics:

  Combinatorics -> Product Rule / Rule of Product Set Theory
  Sources:
  • Young Mathematician Olympiad, 2019-2020, Stage A, Grades 5-6 Question 7

• THE PEAL OF BELLS

  A correspondent, who is apparently much interested in campanology, asks me how he is to construct what he calls a "true and correct" peal for four bells. He says that every possible permutation of the four bells must be rung once, and once only. He adds that no bell must move more than one place at a time, that no bell must make more than two successive strokes in either the first or the last place, and that the last change must be able to pass into the first. These fantastic conditions will be found to be observed in the little peal for three bells, as follows:—

  1	2	3
  2	1	3
  2	3	1
  3	2	1
  3	1	2
  1	3	2

  How are we to give him a correct solution for his four bells?

  Topics:

  Combinatorics -> Product Rule / Rule of Product
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 268

• THE GLASS BALLS

  A number of clever marksmen were staying at a country house, and the host, to provide a little amusement, suspended strings of glass balls, as shown in the illustration, to be fired at. After they had all put their skill to a sufficient test, somebody asked the following question: "What is the total number of different ways in which these sixteen balls may be broken, if we must always break the lowest ball that remains on any string?" Thus, one way would be to break all the four balls on each string in succession, taking the strings from left to right. Another would be to break all the fourth balls on the four strings first, then break the three remaining on the first string, then take the balls on the three other strings alternately from right to left, and so on. There is such a vast number of different ways (since every little variation of order makes a different way) that one is apt to be at first impressed by the great difficulty of the problem. Yet it is really quite simple when once you have hit on the proper method of attacking it. How many different ways are there?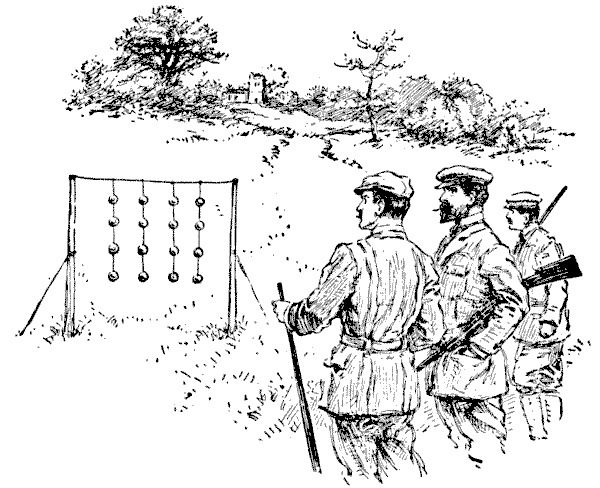
  Topics:

  Combinatorics -> Product Rule / Rule of Product
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 270

• COUNTER CROSSES

  All that we need for this puzzle is nine counters, numbered `1, 2, 3, 4, 5, 6, 7, 8`, and `9`. It will be seen that in the illustration A these are arranged so as to form a Greek cross, while in the case of B they form a Latin cross. In both cases the reader will find that the sum of the numbers in the upright of the cross is the same as the sum of the numbers in the horizontal arm. It is quite easy to hit on such an arrangement by trial, but the problem is to discover in exactly how many different ways it may be done in each case. Remember that reversals and reflections do not count as different. That is to say, if you turn this page round you get four arrangements of the Greek cross, and if you turn it round again in front of a mirror you will get four more. But these eight are all regarded as one and the same. Now, how many different ways are there in each case?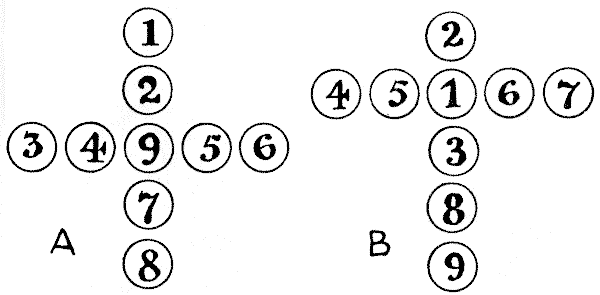
  Topics:

  Combinatorics -> Product Rule / Rule of Product Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Number Tables
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 277