Set Theory

Set theory is the foundational mathematical theory of sets, or collections of objects. It deals with operations on sets (union, intersection, complement, difference), properties of sets (cardinality, subsets), and relations between sets. Questions involve Venn diagrams, set notation, and properties.

• Question

  On the circle, there are blue and red points. It is allowed to add a red point and change the colors of its neighboring points or remove a red point and change the colors of its neighboring points (it is not allowed to leave fewer than 2 points on the circle). Prove that it is impossible to move, using only these operations, from a circle with two red points to a circle with two blue points.
  K. Kaznvosky

  Topics:

  Combinatorics -> Combinatorial Geometry Combinatorics -> Invariants Algebra Logic -> Reasoning / Logic Number Theory -> Division -> Parity (Even/Odd) Set Theory Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Colorings -> Chessboard Coloring
  Sources:
  • Tournament of Towns, 1979-1980, Main, Spring Question 1

• Question

  A group of children went to an amusement park. It is known that the number of girls wearing hats is equal to the number of boys not wearing hats.

  Who are there more of in this group: children not wearing hats or girls?

  Topics:

  Logic -> Reasoning / Logic Set Theory
  Sources:
  • problems.ru web site

• Mitzi

  There are many cats named Mitzi. Which is more numerous: cats excluding the cats that are not named Mitzi, or animals named Mitzi excluding those that are not cats?

  Topics:

  Logic -> Reasoning / Logic Set Theory
  Sources:
  • problems.ru web site

• Pine Trees in the Forest

  A forester counts pine trees in a forest. He walked along each of the circles in the image, and within each circle he counted exactly `3` pine trees. Prove that the forester surely made a mistake in his count.

  

  Topics:

  Logic -> Reasoning / Logic Set Theory Proof and Example -> Proof by Contradiction

• The Clubs

  In the grade, there are `70` children. Of these, `27` go to theater club, `32` sing in the choir, and `22` do Judo. In the theater club, there are `10` children from the choir, in the choir there are `6` children from Judo, and in Judo there are `8` children who also study theater. Three children also go to theater club, Judo, and sing in the choir. How many children from the grade do not participate in any of these three clubs?

  Topics:

  Arithmetic Combinatorics Algebra -> Word Problems Set Theory

• Question

  Every student in the gymnasium knows at least one of the following two ancient languages: Latin or Ancient Greek. It is known that `85%` of all students know Latin, and `75%` know Greek. What is the percentage of students who know both languages?

  Topics:

  Set Theory Arithmetic -> Percentages

• Question

  Hannah is waiting for a bus. Which of the following three events is most likely to occur:

  1. Hannah waits for the bus for at least one minute,
  2. Hannah waits for the bus for at least two minutes,
  3. Hannah waits for the bus for at least five minutes.
  Topics:

  Logic -> Reasoning / Logic Set Theory Probability Theory

• Question

  How many numbers between `1` and `100` are not divisible by `2` or `5`?

  Topics:

  Arithmetic Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules -> Divisibility Rules by 2, 4, and 8 Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules -> Divisibility Rules by 5 and 25 Number Theory -> Greatest Common Divisor (GCD) and Least Common Multiple (LCM) Set Theory Number Theory -> Division

• Watering Potted Plants

  Hannah and Rachel watered potted plants at home. It is known that each of them watered exactly half the number of potted plants in the house, and it is also known that three potted plants were accidentally watered twice. How many potted plants remain to be watered?

  Topics:

  Algebra -> Word Problems Logic -> Reasoning / Logic Set Theory

• Question

  Two congruent triangles form a Star of David as depicted in the drawing. Prove that the shaded area is equal to the hatched area.

  

  Show hint

  Log in here to receive the hint
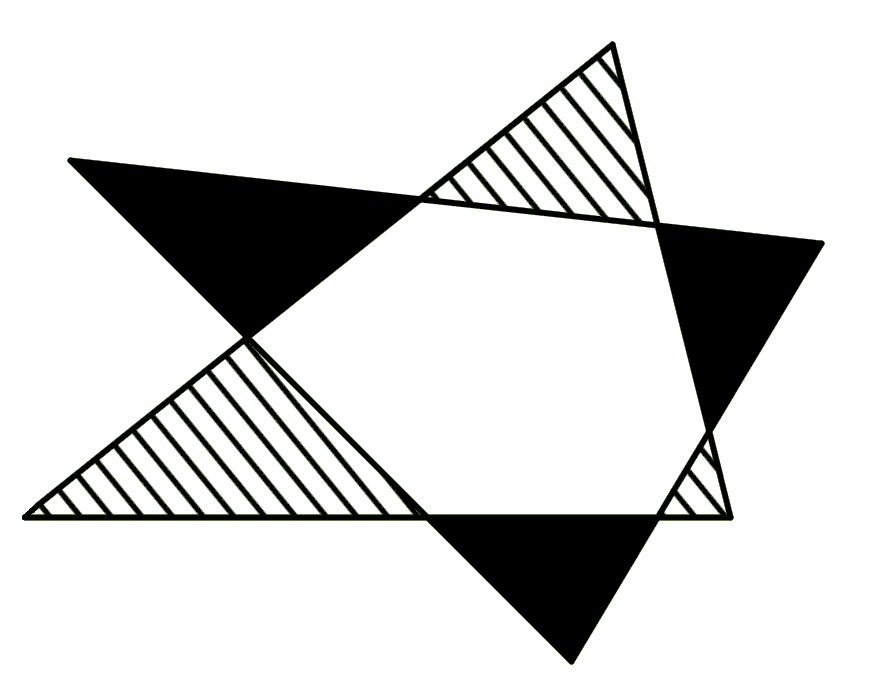  Topics:

  Geometry -> Area Calculation Proof and Example Set Theory Geometry -> Plane Geometry -> Triangles -> Triangle Congruence