Combinatorics, Case Analysis / Checking Cases, Processes / Procedures

This category covers problems involving sequences of operations or steps that evolve over time or iterations. Questions might ask about the outcome of a process, whether it terminates, or properties of its state after a certain number of steps. Often related to algorithms or invariants.

  • Question

    There are 5778 extinguished lamps arranged at equal distances on a circle. Below each lamp is a button. Pressing a button changes the state of 4 lamps: the lamp next to the button, the next two lamps in the circle clockwise, and the lamp opposite the button (an extinguished lamp lights up when its state is changed, and a lit lamp is extinguished). What is the maximum number of lamps that can be lit simultaneously?

    Sources:

  • A PUZZLE IN REVERSALS

    Most people know that if you take any sum of money in pounds, shillings, and pence, in which the number of pounds (less than £`12`) exceeds that of the pence, reverse it (calling the pounds pence and the pence pounds), find the difference, then reverse and add this difference, the result is always £`12, 18`s. `11`d. But if we omit the condition, "less than £`12`," and allow nought to represent shillings or pence—(`1`) What is the lowest amount to which the rule will not apply? (`2`) What is the highest amount to which it will apply? Of course, when reversing such a sum as £`14, 15`s. `3`d. it may be written £`3, 16`s. `2`d., which is the same as £`3, 15`s. `14`d. Sources:

  • DIGITS AND SQUARES

    It will be seen in the diagram that we have so arranged the nine digits in a square that the number in the second row is twice that in the first row, and the number in the bottom row three times that in the top row. There are three other ways of arranging the digits so as to produce the same result. Can you find them? Sources:

  • THE LOCKERS PUZZLE

     

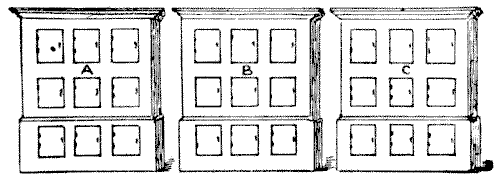
    A man had in his office three cupboards, each containing nine lockers, as shown in the diagram. He told his clerk to place a different one-figure number on each locker of cupboard A, and to do the same in the case of B, and of C. As we are here allowed to call nought a digit, and he was not prohibited from using nought as a number, he clearly had the option of omitting any one of ten digits from each cupboard.

    Now, the employer did not say the lockers were to be numbered in any numerical order, and he was surprised to find, when the work was done, that the figures had apparently been mixed up indiscriminately. Calling upon his clerk for an explanation, the eccentric lad stated that the notion had occurred to him so to arrange the figures that in each case they formed a simple addition sum, the two upper rows of figures producing the sum in the lowest row. But the most surprising point was this: that he had so arranged them that the addition in A gave the smallest possible sum, that the addition in C gave the largest possible sum, and that all the nine digits in the three totals were different. The puzzle is to show how this could be done. No decimals are allowed and the nought may not appear in the hundreds place.

    Sources:

  • THE THREE GROUPS

    There appeared in "Nouvelles Annales de Mathématiques" the following puzzle as a modification of one of my "Canterbury Puzzles." Arrange the nine digits in three groups of two, three, and four digits, so that the first two numbers when multiplied together make the third. Thus, `12` × `483` = `5,796`. I now also propose to include the cases where there are one, four, and four digits, such as `4` × `1,738` = `6,952`. Can you find all the possible solutions in both cases? Sources:

  • THE NINE COUNTERS

    I have nine counters, each bearing one of the nine digits, `1, 2, 3, 4, 5, 6, 7, 8` and `9`. I arranged them on the table in two groups, as shown in the illustration, so as to form two multiplication sums, and found that both sums gave the same product. You will find that `158` multiplied by `23` is `3,634`, and that `79` multiplied by `46` is also `3,634`. Now, the puzzle I propose is to rearrange the counters so as to get as large a product as possible. What is the best way of placing them? Remember both groups must multiply to the same amount, and there must be three counters multiplied by two in one case, and two multiplied by two counters in the other, just as at present. Sources:

  • THE TEN COUNTERS

    In this case we use the nought in addition to the `1, 2, 3, 4, 5, 6, 7, 8, 9`. The puzzle is, as in the last case, so to arrange the ten counters that the products of the two multiplications shall be the same, and you may here have one or more figures in the multiplier, as you choose. The above is a very easy feat; but it is also required to find the two arrangements giving pairs of the highest and lowest products possible. Of course every counter must be used, and the cipher may not be placed to the left of a row of figures where it would have no effect. Vulgar fractions or decimals are not allowed. Sources:

  • DIGITAL MULTIPLICATION

    Here is another entertaining problem with the nine digits, the nought being excluded. Using each figure once, and only once, we can form two multiplication sums that have the same product, and this may be done in many ways. For example, 7x658 and 14x329 contain all the digits once, and the product in each case is the same—`4,606`. Now, it will be seen that the sum of the digits in the product is `16`, which is neither the highest nor the lowest sum so obtainable. Can you find the solution of the problem that gives the lowest possible sum of digits in the common product? Also that which gives the highest possible sum? Sources:

  • THE PIERROT'S PUZZLE

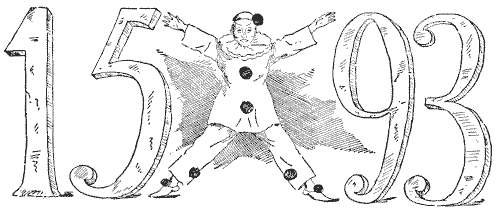    The Pierrot in the illustration is standing in a posture that represents the sign of multiplication. He is indicating the peculiar fact that `15` multiplied by `93` produces exactly the same figures (`1,395`), differently arranged. The puzzle is to take any four digits you like (all different) and similarly arrange them so that the number formed on one side of the Pierrot when multiplied by the number on the other side shall produce the same figures. There are very few ways of doing it, and I shall give all the cases possible. Can you find them all? You are allowed to put two figures on each side of the Pierrot as in the example shown, or to place a single figure on one side and three figures on the other. If we only used three digits instead of four, the only possible ways are these: `3` multiplied by `51` equals `153`, and `6` multiplied by `21` equals `126`. Sources:

  • THE NUMBER CHECKS PUZZLE

    Where a large number of workmen are employed on a building it is customary to provide every man with a little disc bearing his number. These are hung on a board by the men as they arrive, and serve as a check on punctuality. Now, I once noticed a foreman remove a number of these checks from his board and place them on a split-ring which he carried in his pocket. This at once gave me the idea for a good puzzle. In fact, I will confide to my readers that this is just how ideas for puzzles arise. You cannot really create an idea: it happens—and you have to be on the alert to seize it when it does so happen.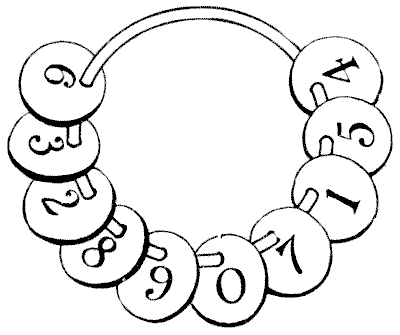 It will be seen from the illustration that there are ten of these checks on a ring, numbered `1` to `9` and `0`. The puzzle is to divide them into three groups without taking any off the ring, so that the first group multiplied by the second makes the third group. For example, we can divide them into the three groups, `2`—`8` `9` `7`—`1` `5` `4` `6` `3`, by bringing the `6` and the `3` round to the `4`, but unfortunately the first two when multiplied together do not make the third. Can you separate them correctly? Of course you may have as many of the checks as you like in any group. The puzzle calls for some ingenuity, unless you have the luck to hit on the answer by chance. Sources: