Combinatorics, Colorings

Coloring problems involve assigning 'colors' (labels) to objects (like regions of a map, vertices/edges of a graph, or squares on a board) subject to certain constraints (e.g., adjacent objects must have different colors). Questions ask if a coloring is possible or seek the minimum number of colors.

Chessboard Coloring

  • Two Hashes

    What is the maximum number of "domino" shapes (rectangles `1 times 2` or `2 times 1`) that can be placed inside the orange shape,
    such that they do not overlap and do not extend beyond the boundaries of the shape?

    Sources:

  • THE GRAND LAMA'S PROBLEM

    Once upon a time there was a Grand Lama who had a chessboard made of pure gold, magnificently engraved, and, of course, of great value. Every year a tournament was held at Lhassa among the priests, and whenever any one beat the Grand Lama it was considered a great honour, and his name was inscribed on the back of the board, and a costly jewel set in the particular square on which the checkmate had been given. After this sovereign pontiff had been defeated on four occasions he died—possibly of chagrin.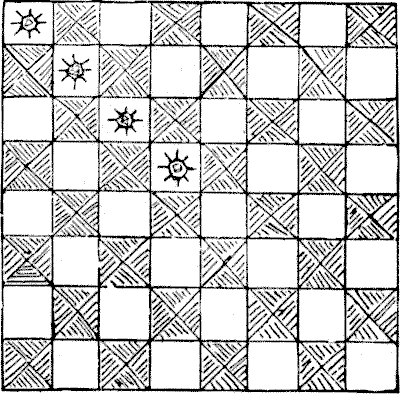 Now the new Grand Lama was an inferior chess-player, and preferred other forms of innocent amusement, such as cutting off people's heads. So he discouraged chess as a degrading game, that did not improve either the mind or the morals, and abolished the tournament summarily. Then he sent for the four priests who had had the effrontery to play better than a Grand Lama, and addressed them as follows: "Miserable and heathenish men, calling yourselves priests! Know ye not that to lay claim to a capacity to do anything better than my predecessor is a capital offence? Take that chessboard and, before day dawns upon the torture chamber, cut it into four equal parts of the same shape, each containing sixteen perfect squares, with one of the gems in each part! If in this you fail, then shall other sports be devised for your special delectation. Go!" The four priests succeeded in their apparently hopeless task. Can you show how the board may be divided into four equal parts, each of exactly the same shape, by cuts along the lines dividing the squares, each part to contain one of the gems? Sources:

  • THE CHESSBOARD SENTENCE

     

    I once set myself the amusing task of so dissecting an ordinary chessboard into letters of the alphabet that they would form a complete sentence. It will be seen from the illustration that the pieces assembled give the sentence, "CUT THY LIFE," with the stops between. The ideal sentence would, of course, have only one full stop, but that I did not succeed in obtaining.

    The sentence is an appeal to the transgressor to cut himself adrift from the evil life he is living. Can you fit these pieces together to form a perfect chessboard?

    Sources:

  • BISHOPS—UNGUARDED

    Place as few bishops as possible on an ordinary chessboard so that every square of the board shall be either occupied or attacked. It will be seen that the rook has more scope than the bishop: for wherever you place the former, it will always attack fourteen other squares; whereas the latter will attack seven, nine, eleven, or thirteen squares, according to the position of the diagonal on which it is placed. And it is well here to state that when we speak of "diagonals" in connection with the chessboard, we do not limit ourselves to the two long diagonals from corner to corner, but include all the shorter lines that are parallel to these. To prevent misunderstanding on future occasions, it will be well for the reader to note carefully this fact. Sources:

  • BISHOPS—GUARDED

    Now, how many bishops are necessary in order that every square shall be either occupied or attacked, and every bishop guarded by another bishop? And how may they be placed? Sources:

  • UNDER THE VEIL

    If the reader will examine the above diagram, he will see that I have so placed eight V's, eight E's, eight I's, and eight L's in the diagram that no letter is in line with a similar one horizontally, vertically, or diagonally. Thus, no V is in line with another V, no E with another E, and so on. There are a great many different ways of arranging the letters under this condition. The puzzle is to find an arrangement that produces the greatest possible number of four-letter words, reading upwards and downwards, backwards and forwards, or diagonally. All repetitions count as different words, and the five variations that may be used are: VEIL, VILE, LEVI, LIVE, and EVIL.

    This will be made perfectly clear when I say that the above arrangement scores eight, because the top and bottom row both give VEIL; the second and seventh columns both give VEIL; and the two diagonals, starting from the L in the 5th row and E in the 8th row, both give LIVE and EVIL. There are therefore eight different readings of the words in all.

    This difficult word puzzle is given as an example of the use of chessboard analysis in solving such things. Only a person who is familiar with the "Eight Queens" problem could hope to solve it.

    Sources:

  • AN EPISCOPAL VISITATION

    The white squares on the chessboard represent the parishes of a diocese. Place the bishop on any square you like, and so contrive that (using the ordinary bishop's move of chess) he shall visit every one of his parishes in the fewest possible moves. Of course, all the parishes passed through on any move are regarded as "visited." You can visit any squares more than once, but you are not allowed to move twice between the same two adjoining squares. What are the fewest possible moves? The bishop need not end his visitation at the parish from which he first set out. Sources:

  • THE QUEEN'S TOUR

    The puzzle of making a complete tour of the chessboard with the queen in the fewest possible moves (in which squares may be visited more than once) was first given by the late Sam Loyd in his Chess Strategy. But the solution shown below is the one he gave in American Chess-Nuts in `1868`. I have recorded at least six different solutions in the minimum number of moves—fourteen—but this one is the best of all, for reasons I will explain.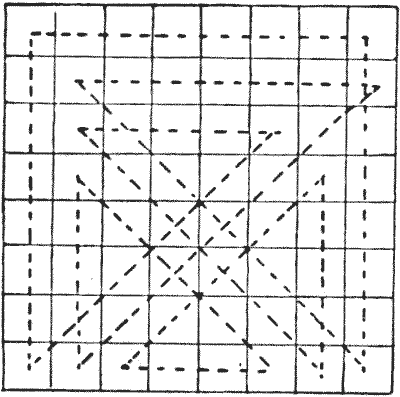 If you will look at the lettered square you will understand that there are only ten really differently placed squares on a chessboard—those enclosed by a dark line—all the others are mere reversals or reflections. For example, every A is a corner square, and every J a central square. Consequently, as the solution shown has a turning-point at the enclosed D square, we can obtain a solution starting from and ending at any square marked D—by just turning the board about. Now, this scheme will give you a tour starting from any A, B, C, D, E, F, or H, while no other route that I know can be adapted to more than five different starting-points. There is no Queen's Tour in fourteen moves (remember a tour must be re-entrant) that may start from a G, I, or J. But we can have a non-re-entrant path over the whole board in fourteen moves, starting from any given square. Hence the following puzzle:— 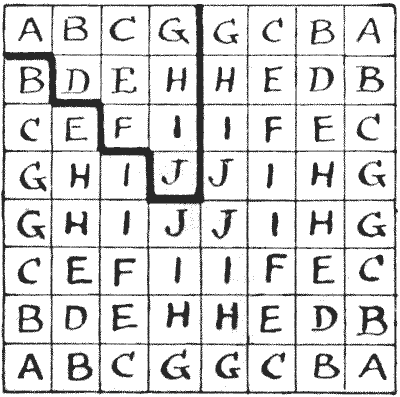Start from the J in the enclosed part of the lettered diagram and visit every square of the board in fourteen moves, ending wherever you like. Sources:

  • THE FOUR KANGAROOS

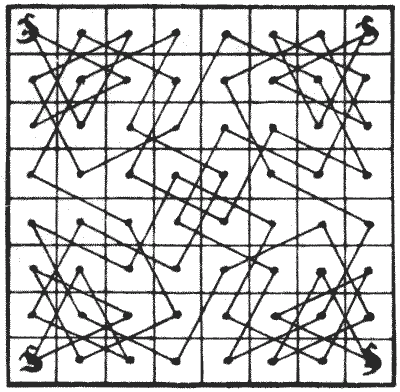    In introducing a little Commonwealth problem, I must first explain that the diagram represents the sixty-four fields, all properly fenced off from one another, of an Australian settlement, though I need hardly say that our kith and kin "down under" always do set out their land in this methodical and exact manner. It will be seen that in every one of the four corners is a kangaroo. Why kangaroos have a marked preference for corner plots has never been satisfactorily explained, and it would be out of place to discuss the point here. I should also add that kangaroos, as is well known, always leap in what we call "knight's moves." In fact, chess players would probably have adopted the better term "kangaroo's move" had not chess been invented before kangaroos.

    The puzzle is simply this. One morning each kangaroo went for his morning hop, and in sixteen consecutive knight's leaps visited just fifteen different fields and jumped back to his corner. No field was visited by more than one of the kangaroos. The diagram shows how they arranged matters. What you are asked to do is to show how they might have performed the feat without any kangaroo ever crossing the horizontal line in the middle of the square that divides the board into two equal parts.

    Sources:

  • THE TWO ROOKS

    This is a puzzle game for two players. Each player has a single rook. The first player places his rook on any square of the board that he may choose to select, and then the second player does the same. They now play in turn, the point of each play being to capture the opponent's rook. But in this game you cannot play through a line of attack without being captured. That is to say, if in the diagram it is Black's turn to play, he cannot move his rook to his king's knight's square, or to his king's rook's square, because he would enter the "line of fire" when passing his king's bishop's square. For the same reason he cannot move to his queen's rook's seventh or eighth squares. Now, the game can never end in a draw. Sooner or later one of the rooks must fall, unless, of course, both players commit the absurdity of not trying to win. The trick of winning is ridiculously simple when you know it. Can you solve the puzzle? Sources: