Combinatorics, Colorings, Chessboard Coloring

Chessboard coloring uses the alternating black and white pattern of a standard chessboard (or similar grid colorings) as a tool to solve problems, particularly those involving tiling, covering, or movement on grids. It's a specific application of invariant or parity arguments.

• Question

  On the circle, there are blue and red points. It is allowed to add a red point and change the colors of its neighboring points or remove a red point and change the colors of its neighboring points (it is not allowed to leave fewer than 2 points on the circle). Prove that it is impossible to move, using only these operations, from a circle with two red points to a circle with two blue points.
  K. Kaznvosky

  Topics:

  Combinatorics -> Combinatorial Geometry Combinatorics -> Invariants Algebra Logic -> Reasoning / Logic Number Theory -> Division -> Parity (Even/Odd) Set Theory Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Colorings -> Chessboard Coloring
  Sources:
  • Tournament of Towns, 1979-1980, Main, Spring Question 1

• Question

  Is it possible to tile a `5xx5` board with dominoes?

  Note: The size of a board square matches the size of a domino square.

  Topics:

  Combinatorics -> Combinatorial Geometry Logic -> Reasoning / Logic Number Theory -> Division -> Parity (Even/Odd) Combinatorics -> Colorings -> Chessboard Coloring

• Question

  A knight exited the square `a1` and, after several moves, returned to the same square.

  Is it possible that the knight made an odd number of moves?

  Show hint

  Log in here to receive the hint
  Topics:

  Combinatorics -> Invariants Logic -> Reasoning / Logic Number Theory -> Division -> Parity (Even/Odd) Combinatorics -> Colorings -> Chessboard Coloring

• Question

  A knight moves from square `a1` to square `h8`. Is it possible that along the way it visited every square on the board exactly once?

  Show hint

  Log in here to receive the hint
  Topics:

  Combinatorics -> Double Counting Combinatorics -> Invariants Combinatorics -> Graph Theory Logic -> Reasoning / Logic Number Theory -> Division -> Parity (Even/Odd) Proof and Example -> Proof by Contradiction Combinatorics -> Colorings -> Chessboard Coloring

• Question

  From a chessboard, two opposite corners are removed (the squares `a1` and `h8`, for example). Can you tile the remaining board with dominoes?

  Show hint

  Log in here to receive the hint
  Topics:

  Combinatorics -> Invariants Combinatorics -> Matchings Logic -> Reasoning / Logic Number Theory -> Division -> Parity (Even/Odd) Proof and Example -> Proof by Contradiction Combinatorics -> Colorings -> Chessboard Coloring Puzzles and Rebuses

• Question

  Prove that the given shape cannot be cut into dominoes:

  

  Topics:

  Combinatorics -> Invariants Combinatorics -> Matchings Number Theory -> Division -> Parity (Even/Odd) Proof and Example -> Proof by Contradiction Combinatorics -> Colorings -> Chessboard Coloring Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems

• Question

  Can you cut the shape on the left into six shapes like the shape on the right?

  

  Topics:

  Combinatorics -> Invariants Combinatorics -> Matchings Proof and Example Combinatorics -> Colorings -> Chessboard Coloring Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry

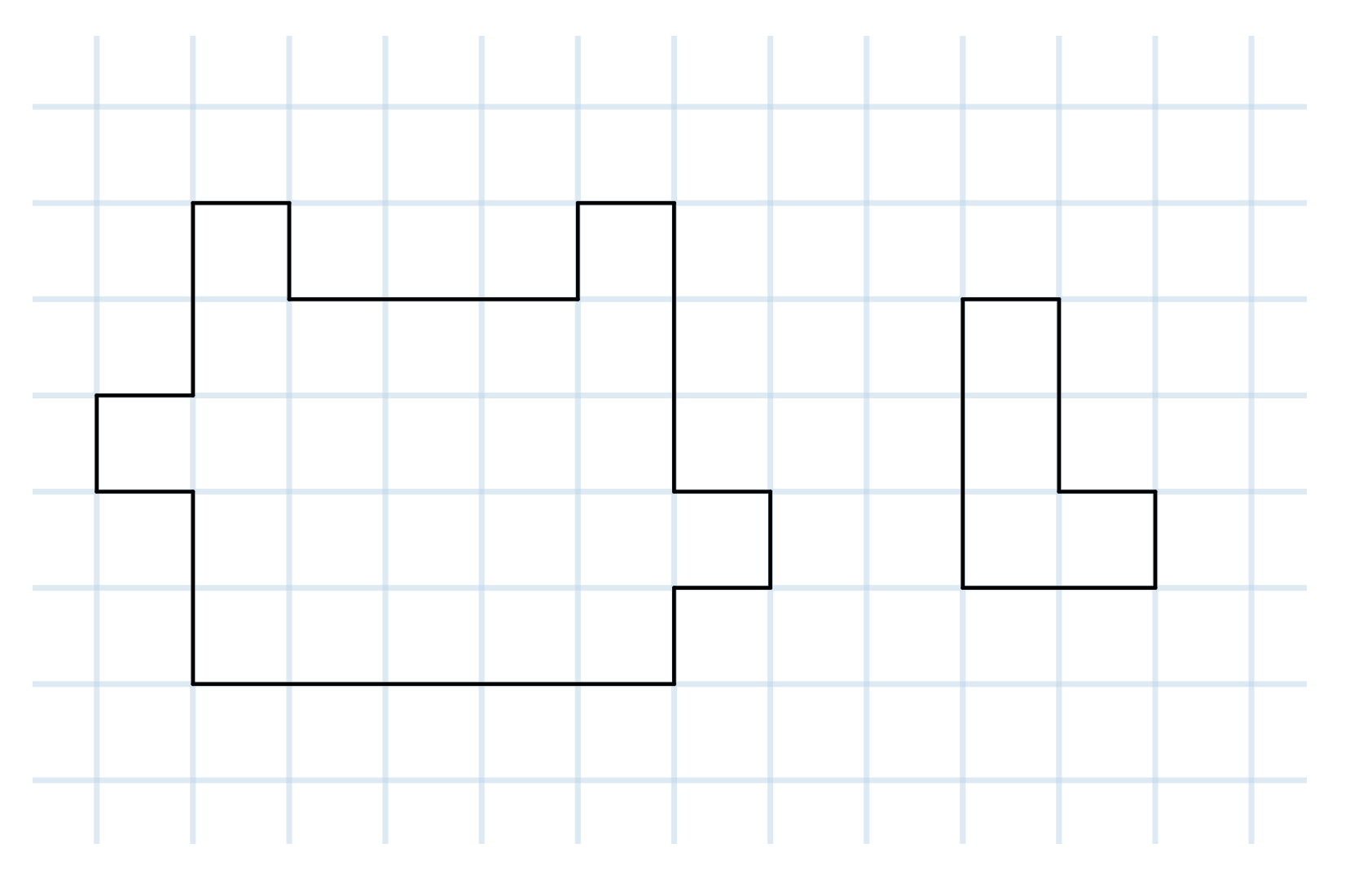
• Question

  Shlomi has a chessboard and a cube whose face size is the same as the size of a square on the board. Shlomi wants to paint the faces of the cube black and white, and then roll the cube across the board so that each time the face touching the board is the same color as the square it touches. The cube is supposed to pass through each square on the board exactly once. Can Shlomi do this? Justify or provide an example.

  Topics:

  Combinatorics -> Combinatorial Geometry Combinatorics -> Graph Theory Logic -> Reasoning / Logic Proof and Example -> Proof by Contradiction Combinatorics -> Colorings -> Chessboard Coloring

• Differences in the Multiplication Table

  Color the `10xx10` multiplication table with a black and white chessboard coloring, such that the cell of `1xx1` is colored black.
  Find the difference between the sum of all the numbers in the black cells and the sum of all the numbers in the white cells.
   

  	1	2	3	4	5	6	7	8	9	10
  1	1	2	3	4	5	6	7	8	9	10
  2	2	4	6	8	10	12	14	16	18	20
  3	3	6	9	12	15	18	21	24	27	30
  4	4	8	12	16	20	24	28	32	36	40
  5	5	10	15	20	25	30	35	40	45	50
  6	6	12	18	24	30	36	42	48	54	60
  7	7	14	21	28	35	42	49	56	63	70
  8	8	16	24	32	40	48	56	64	72	80
  9	9	18	27	36	45	54	63	72	81	90
  10	10	20	30	40	50	60	70	80	90	100

  Show hint

  Log in here to receive the hint
  Topics:

  Arithmetic Combinatorics -> Number Tables Combinatorics -> Colorings -> Chessboard Coloring
  Sources:
  • Young Mathematician Olympiad, 2017-2018, Stage A, Grades 3-4 Question 8
  • Young Mathematician Olympiad, 2017-2018, Stage A, Grades 5-6 Question 8

• The Grasshopper

  Consider an infinite grid of squares. A grasshopper sits on one of the squares. The grasshopper can jump two squares in any horizontal or vertical direction, and it can jump to the adjacent square diagonally. Can the grasshopper ever reach a square that is adjacent to its starting square by a side?

  Topics:

  Combinatorics -> Combinatorial Geometry Combinatorics -> Invariants Combinatorics -> Colorings -> Chessboard Coloring
  Sources:
  • Young Mathematician Olympiad, 2017-2018, Final, Grades 3-4 Question 2