טבעות הברזל המייגעות

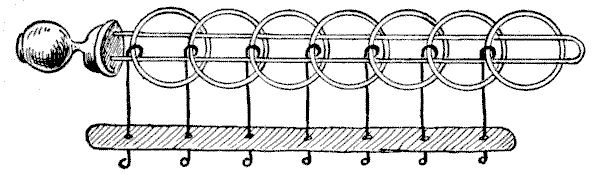
האיור מייצג אחד מהחידות המכאניות העתיקות ביותר. מקורו אינו ידוע. קרדנו, המתמטיקאי, כתב עליו בשנת `1550`, וואליס בשנת `1693`; בעוד שאומרים שהוא עדיין נמצא בכפרים אנגליים נידחים (לפעמים מונח במקומות מוזרים, כמו מגדל פעמונים של כנסייה), עשוי מברזל, ונקרא באופן הולם "טבעות מייגעות", ומשמש את הנורווגים כיום כמנעול לקופסאות ותיקים. בחנויות הצעצועים הוא נקרא לפעמים "טבעות סיניות", אם כי נראה שאין סמכות לתיאור, ולרוב הוא מכונה בשם הלא מספק "הטבעות המבלבלות". הצרפתים קוראים לזה "Baguenaudier."

ניתן לראות שהחידה מורכבת מ-לולאה פשוטה של חוט המקובעת בידית שאותה מחזיקים ביד שמאל, וממספר מסוים של טבעות המאובטחות על ידי חוטים העוברים דרך חורים ב-מוט ונשמרים שם על ידי קצותיהם הקהים. החוטים פועלים בחופשיות במוט, אך אינם יכולים להיפרד ממנו, וגם לא ניתן להסיר את החוטים מהטבעות. החידה הכללית היא לנתק את הלולאה לחלוטין מכל הטבעות, ואז להחזיר את כולן שוב.

כעת, ניתן לראות במבט חטוף שניתן להסיר את הטבעת הראשונה (מימין) בכל עת על ידי החלקתה מעל הקצה והשלכתה דרך הלולאה; או שאפשר להחזיר אותה על ידי היפוך הפעולה. מלבד זאת, הטבעת היחידה שניתן להסיר אי פעם היא זו שבמקרה נמצאת השנייה הסמוכה על הלולאה בקצה הימני. כך, כשכל הטבעות עליה, ניתן להפיל את השנייה מיד; כשהטבעת הראשונה למטה, אינך יכול להפיל את השנייה, אך תוכל להסיר את השלישית; כששלוש הטבעות הראשונות למטה, אינך יכול להפיל את הרביעית, אך תוכל להסיר את החמישית; וכן הלאה. יתברר שאפשר להפיל את הטבעות הראשונה והשנייה יחד או להחזיר אותן יחד; אך כדי למנוע בלבול, לא נאפשר את המהלך הכפול החריג הזה, ונגיד שניתן להחזיר או להסיר רק טבעת אחת בכל פעם.

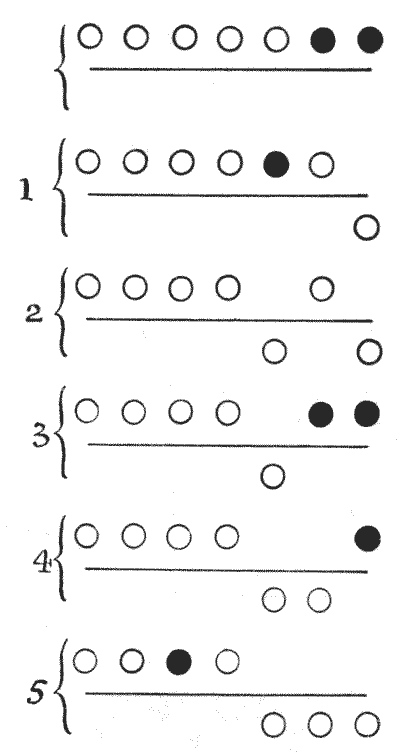
אנו יכולים להסיר טבעת אחת ב-`1` מהלך; שתי טבעות ב-`2` מהלכים; שלוש טבעות ב-`5` מהלכים; ארבע טבעות ב-`10` מהלכים; חמש טבעות ב-`21` מהלכים; ואם נמשיך להכפיל (ולהוסיף אחד כאשר מספר הטבעות הוא אי-זוגי) נוכל לברר בקלות את מספר המהלכים להסרת כל מספר טבעות לחלוטין. כדי להוריד את כל שבע הטבעות נדרשים `85` מהלכים. בואו נסתכל על חמשת המהלכים שנעשו בהסרת שלוש הטבעות הראשונות, העיגולים מעל הקו מייצגים טבעות על הלולאה ואלה שמתחת מייצגים טבעות מחוץ ללולאה.

הפילו את הטבעת הראשונה; הפילו את השלישית; הרימו את הראשונה; הפילו את השנייה; והפילו את הראשונה—`5` מהלכים, כפי שמוצג בבירור בתרשימים. העיגולים הכהים מראים בכל שלב, ממצב ההתחלה ועד הסיום, אילו טבעות אפשר להפיל. לאחר מהלך `2` יורגש שלא ניתן להפיל אף טבעת עד שאחת תוחזר, מכיוון שהטבעות הראשונה והשנייה מימין שנמצאות כעת על הלולאה אינן יחד. לאחר המהלך החמישי, אם ברצוננו להסיר את כל שבע הטבעות, עלינו כעת להפיל את החמישית. אבל לפני שנוכל להסיר אז את הרביעית, יש צורך להחזיר את שלוש הראשונות ולהסיר את שתי הראשונות. אז יהיו לנו `7, 6, 4, 3` על הלולאה, ולכן נוכל להפיל את הרביעית. כשנחזיר `2` ו-`1` ונסיר `3, 2, 1`, נוכל להפיל את הטבעת השביעית. הפעולה הבאה אז תהיה להשיג `6, 5, 4, 3, 2, 1` על הלולאה ולהסיר `4, 3, 2, 1`, ואז `6` תרד; ואז להשיג `5, 4, 3, 2, 1` על הלולאה, ולהסיר `3, 2, 1`, ואז `5` תרד; ואז להשיג `4, 3, 2, 1` על הלולאה ולהסיר `2, 1`, ואז `4` תרד; ואז להשיג `3, 2, 1` על הלולאה ולהסיר `1`, ואז `3` תרד; ואז להשיג `2, 1` על הלולאה, ואז `2` תרד; ו-`1` תיפול דרך במהלך ה-85, ותשאיר את הלולאה חופשית לחלוטין. על הקורא להיות מסוגל כעת להבין את החידה, בין אם יש לו אותה ביד בצורה מעשית ובין אם לא.

הבעיה המסוימת שאני מציע היא פשוט זו. נניח שיש בסך הכל ארבע עשרה טבעות על טבעות הברזל המייגעות, ואנו ממשיכים להסיר את כולן בצורה הנכונה כדי לא לבזבז אף מהלך. מה יהיה מצב הטבעות לאחר שבוצע המהלך ה-`9`,999?