חידת הלוקרים

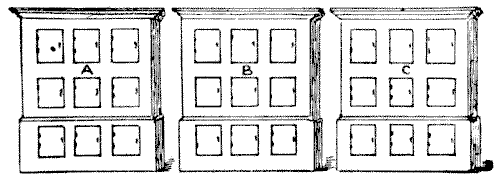
לאיש היו במשרדו שלושה ארונות, שבכל אחד מהם תשעה לוקרים, כפי שמוצג בדיאגרמה. הוא הורה לפקיד שלו להציב ספרה שונה על כל לוקר בארון A, ולעשות את אותו הדבר בארון B ובארון C. מכיוון שמותר לנו כאן לקרוא לאפס ספרה, ולא נאסר עליו להשתמש באפס כמספר, ברור שהייתה לו האפשרות להשמיט כל אחת מעשר הספרות מכל ארון.

כעת, המעסיק לא אמר שהלוקרים ימוספרו בסדר מספרי כלשהו, והוא הופתע לגלות, לאחר שהעבודה הסתיימה, שהספרות כנראה עורבבו באופן אקראי. כשקרא לפקיד שלו להסבר, הנער האקסצנטרי הצהיר שהעלתה בדעתו המחשבה לסדר את הספרות כך שבכל מקרה הן יצרו תרגיל חיבור פשוט, כאשר שתי השורות העליונות של הספרות יוצרות את הסכום בשורה התחתונה. אבל הנקודה המפתיעה ביותר הייתה זו: שהוא סידר אותן כך שהחיבור ב-A נתן את הסכום הקטן ביותר האפשרי, שהחיבור ב-C נתן את הסכום הגדול ביותר האפשרי, וכי כל תשע הספרות בסך הכל בשלושת הסכומים היו שונות. החידה היא להראות כיצד ניתן לעשות זאת. אין לאפשר עשרונים והאפס אינו יכול להופיע במקום המאות.