THE PENTAGON AND SQUARE

I wonder how many of my readers, amongst those who have not given any close attention to the elements of geometry, could draw a regular pentagon, or five-sided figure, if they suddenly required to do so. A regular hexagon, or six-sided figure, is easy enough, for everybody knows that all you have to do is to describe a circle and then, taking the radius as the length of one of the sides, mark off the six points round the circumference. But a pentagon is quite another matter. So, as my puzzle has to do with the cutting up of a regular pentagon, it will perhaps be well if I first show my less experienced readers how this figure is to be correctly drawn. Describe a circle and draw the two lines H B and D G, in the diagram, through the centre at right angles. Now find the point A, midway between C and B. Next place the point of your compasses at A and with the distance A D describe the arc cutting H B at E. Then place the point of your compasses at D and with the distance D E describe the arc cutting the circumference at F. Now, D F is one of the sides of your pentagon, and you have simply to mark off the other sides round the circle. Quite simple when you know how, but otherwise somewhat of a poser. 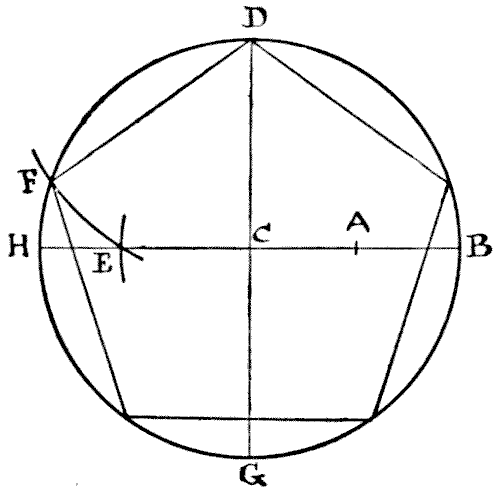Having formed your pentagon, the puzzle is to cut it into the fewest possible pieces that will fit together and form a perfect square.