Amusements in Mathematics, Henry Ernest Dudeney

  • Question 131 - THE SPANISH MISER

    There once lived in a small town in New Castile a noted miser named Don Manuel Rodriguez. His love of money was only equalled by a strong passion for arithmetical problems. These puzzles usually dealt in some way or other with his accumulated treasure, and were propounded by him solely in order that he might have the pleasure of solving them himself. Unfortunately very few of them have survived, and when travelling through Spain, collecting material for a proposed work on "The Spanish Onion as a Cause of National Decadence," I only discovered a very few. One of these concerns the three boxes that appear in the accompanying authentic portrait. Each box contained a different number of golden doubloons. The difference between the number of doubloons in the upper box and the number in the middle box was the same as the difference between the number in the middle box and the number in the bottom box. And if the contents of any two of the boxes were united they would form a square number. What is the smallest number of doubloons that there could have been in any one of the boxes?

  • Question 132 - THE NINE TREASURE BOXES

    The following puzzle will illustrate the importance on occasions of being able to fix the minimum and maximum limits of a required number. This can very frequently be done. For example, it has not yet been ascertained in how many different ways the knight's tour can be performed on the chess board; but we know that it is fewer than the number of combinations of `168` things taken `63` at a time and is greater than `31,054,144`—for the latter is the number of routes of a particular type. Or, to take a more familiar case, if you ask a man how many coins he has in his pocket, he may tell you that he has not the slightest idea. But on further questioning you will get out of him some such statement as the following: "Yes, I am positive that I have more than three coins, and equally certain that there are not so many as twenty-five." Now, the knowledge that a certain number lies between `2` and `12` in my puzzle will enable the solver to find the exact answer; without that information there would be an infinite number of answers, from which it would be impossible to select the correct one.

    This is another puzzle received from my friend Don Manuel Rodriguez, the cranky miser of New Castile. On New Year's Eve in `1879` he showed me nine treasure boxes, and after informing me that every box contained a square number of golden doubloons, and that the difference between the contents of A and B was the same as between B and C, D and E, E and F, G and H, or H and I, he requested me to tell him the number of coins in every one of the boxes. At first I thought this was impossible, as there would be an infinite number of different answers, but on consideration I found that this was not the case. I discovered that while every box contained coins, the contents of A, B, C increased in weight in alphabetical order; so did D, E, F; and so did G, H, I; but D or E need not be heavier than C, nor G or H heavier than F. It was also perfectly certain that box A could not contain more than a dozen coins at the outside; there might not be half that number, but I was positive that there were not more than twelve. With this knowledge I was able to arrive at the correct answer.

    In short, we have to discover nine square numbers such that A, B, C; and D, E, F; and G, H, I are three groups in arithmetical progression, the common difference being the same in each group, and A being less than `12`. How many doubloons were there in every one of the nine boxes?

  • Question 133 - THE FIVE BRIGANDS

    The five Spanish brigands, Alfonso, Benito, Carlos, Diego, and Esteban, were counting their spoils after a raid, when it was found that they had captured altogether exactly `200` doubloons. One of the band pointed out that if Alfonso had twelve times as much, Benito three times as much, Carlos the same amount, Diego half as much, and Esteban one-third as much, they would still have altogether just `200` doubloons. How many doubloons had each?

    There are a good many equally correct answers to this question. Here is one of them:

    A 6 × 12 = 72
    B 12 × 3 = 36
    C 17 × 1 = 17
    D 120 × ½ = 60
    E 45 × 1/3 = 15
      200       200

    The puzzle is to discover exactly how many different answers there are, it being understood that every man had something and that there is to be no fractional money—only doubloons in every case.

    This problem, worded somewhat differently, was propounded by Tartaglia (died `1559`), and he flattered himself that he had found one solution; but a French mathematician of note (M.A. Labosne), in a recent work, says that his readers will be astonished when he assures them that there are `6,639` different correct answers to the question. Is this so? How many answers are there?

  • Question 134 - THE BANKER'S PUZZLE

    A banker had a sporting customer who was always anxious to wager on anything. Hoping to cure him of his bad habit, he proposed as a wager that the customer would not be able to divide up the contents of a box containing only sixpences into an exact number of equal piles of sixpences. The banker was first to put in one or more sixpences (as many as he liked); then the customer was to put in one or more (but in his case not more than a pound in value), neither knowing what the other put in. Lastly, the customer was to transfer from the banker's counter to the box as many sixpences as the banker desired him to put in. The puzzle is to find how many sixpences the banker should first put in and how many he should ask the customer to transfer, so that he may have the best chance of winning.

  • Question 135 - THE STONEMASON'S PROBLEM

    A stonemason once had a large number of cubic blocks of stone in his yard, all of exactly the same size. He had some very fanciful little ways, and one of his queer notions was to keep these blocks piled in cubical heaps, no two heaps containing the same number of blocks. He had discovered for himself (a fact that is well known to mathematicians) that if he took all the blocks contained in any number of heaps in regular order, beginning with the single cube, he could always arrange those on the ground so as to form a perfect square. This will be clear to the reader, because one block is a square, `1+8 = 9` is a square, `1+8+27=36` is a square, `1+8+27+64=100` is a square, and so on. In fact, the sum of any number of consecutive cubes, beginning always with `1`, is in every case a square number.

    One day a gentleman entered the mason's yard and offered him a certain price if he would supply him with a consecutive number of these cubical heaps which should contain altogether a number of blocks that could be laid out to form a square, but the buyer insisted on more than three heaps and declined to take the single block because it contained a flaw. What was the smallest possible number of blocks of stone that the mason had to supply?

  • Question 136 - THE SULTAN'S ARMY

    A certain Sultan wished to send into battle an army that could be formed into two perfect squares in twelve different ways. What is the smallest number of men of which that army could be composed? To make it clear to the novice, I will explain that if there were `130` men, they could be formed into two squares in only two different ways—`81` and `49`, or `121` and `9`. Of course, all the men must be used on every occasion.

  • Question 137 - A STUDY IN THRIFT

    Certain numbers are called triangular, because if they are taken to represent counters or coins they may be laid out on the table so as to form triangles. The number `1` is always regarded as triangular, just as `1` is a square and a cube number. Place one counter on the table—that is, the first triangular number. Now place two more counters beneath it, and you have a triangle of three counters; therefore `3` is triangular. Next place a row of three more counters, and you have a triangle of six counters; therefore `6` is triangular. We see that every row of counters that we add, containing just one more counter than the row above it, makes a larger triangle.

    Now, half the sum of any number and its square is always a triangular number. Thus half of `2` + `2``2` = `3`; half of `3` + `3``2` = `6`; half of `4 + 4``2` = `10`; half of `5` + `5``2`= `15`; and so on. So if we want to form a triangle with `8` counters on each side we shall require half of `8 + 8``2`, or `36` counters. This is a pretty little property of numbers. Before going further, I will here say that if the reader refers to the "Stonemason's Problem" (No. `135`) he will remember that the sum of any number of consecutive cubes beginning with `1` is always a square, and these form the series `1``2`, `3``2`, `6``2`, `10``2`, etc. It will now be understood when I say that one of the keys to the puzzle was the fact that these are always the squares of triangular numbers—that is, the squares of `1, 3, 6, 10, 15, 21, 28`, etc., any of which numbers we have seen will form a triangle.

    Every whole number is either triangular, or the sum of two triangular numbers or the sum of three triangular numbers. That is, if we take any number we choose we can always form one, two, or three triangles with them. The number `1` will obviously, and uniquely, only form one triangle; some numbers will only form two triangles (as `2, 4, 11`, etc.); some numbers will only form three triangles (as `5, 8, 14`, etc.). Then, again, some numbers will form both one and two triangles (as `6`), others both one and three triangles (as `3` and `10`), others both two and three triangles (as `7` and `9`), while some numbers (like `21`) will form one, two, or three triangles, as we desire. Now for a little puzzle in triangular numbers.

    Sandy McAllister, of Aberdeen, practised strict domestic economy, and was anxious to train his good wife in his own habits of thrift. He told her last New Year's Eve that when she had saved so many sovereigns that she could lay them all out on the table so as to form a perfect square, or a perfect triangle, or two triangles, or three triangles, just as he might choose to ask he would add five pounds to her treasure. Soon she went to her husband with a little bag of £`36` in sovereigns and claimed her reward. It will be found that the thirty-six coins will form a square (with side `6`), that they will form a single triangle (with side `8`), that they will form two triangles (with sides `5` and `6`), and that they will form three triangles (with sides `3, 5`, and `5`). In each of the four cases all the thirty-six coins are used, as required, and Sandy therefore made his wife the promised present like an honest man.

    The Scotsman then undertook to extend his promise for five more years, so that if next year the increased number of sovereigns that she has saved can be laid out in the same four different ways she will receive a second present; if she succeeds in the following year she will get a third present, and so on until she has earned six presents in all. Now, how many sovereigns must she put together before she can win the sixth present?

    What you have to do is to find five numbers, the smallest possible, higher than `36`, that can be displayed in the four ways—to form a square, to form a triangle, to form two triangles, and to form three triangles. The highest of your five numbers will be your answer.

  • Question 138 - THE ARTILLERYMEN'S DILEMMA

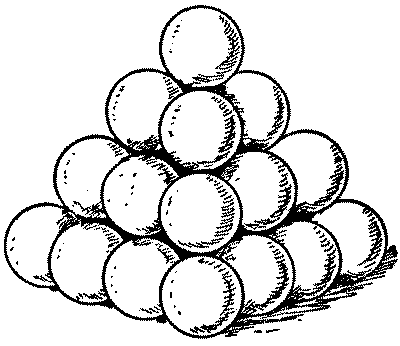    "All cannon-balls are to be piled in square pyramids," was the order issued to the regiment. This was done. Then came the further order, "All pyramids are to contain a square number of balls." Whereupon the trouble arose. "It can't be done," said the major. "Look at this pyramid, for example; there are sixteen balls at the base, then nine, then four, then one at the top, making thirty balls in all. But there must be six more balls, or five fewer, to make a square number." "It must be done," insisted the general. "All you have to do is to put the right number of balls in your pyramids." "I've got it!" said a lieutenant, the mathematical genius of the regiment. "Lay the balls out singly." "Bosh!" exclaimed the general. "You can't pile one ball into a pyramid!" Is it really possible to obey both orders?

  • Question 139 - THE DUTCHMEN'S WIVES

    I wonder how many of my readers are acquainted with the puzzle of the "Dutchmen's Wives"—in which you have to determine the names of three men's wives, or, rather, which wife belongs to each husband. Some thirty years ago it was "going the rounds," as something quite new, but I recently discovered it in the Ladies' Diary for `1739-40`, so it was clearly familiar to the fair sex over one hundred and seventy years ago. How many of our mothers, wives, sisters, daughters, and aunts could solve the puzzle to-day? A far greater proportion than then, let us hope.

    Three Dutchmen, named Hendrick, Elas, and Cornelius, and their wives, Gurtrün, Katrün, and Anna, purchase hogs. Each buys as many as he (or she) gives shillings for one. Each husband pays altogether three guineas more than his wife. Hendrick buys twenty-three more hogs than Katrün, and Elas eleven more than Gurtrün. Now, what was the name of each man's wife?

  • Question 140 - FIND ADA'S SURNAME

    This puzzle closely resembles the last one, my remarks on the solution of which the reader may like to apply in another case. It was recently submitted to a Sydney evening newspaper that indulges in "intellect sharpeners," but was rejected with the remark that it is childish and that they only published problems capable of solution! Five ladies, accompanied by their daughters, bought cloth at the same shop. Each of the ten paid as many farthings per foot as she bought feet, and each mother spent `8`s. `5`¼d. more than her daughter. Mrs. Robinson spent `6`s. more than Mrs. Evans, who spent about a quarter as much as Mrs. Jones. Mrs. Smith spent most of all. Mrs. Brown bought `21` yards more than Bessie—one of the girls. Annie bought `16` yards more than Mary and spent £`3, 0`s. `8`d. more than Emily. The Christian name of the other girl was Ada. Now, what was her surname?