Combinatorics, Invariants
An invariant is a property of a system or mathematical object that remains unchanged when transformations or operations are applied. Identifying an invariant can be key to solving problems about processes or proving impossibility. Questions involve finding such constant quantities or properties.
-
Pumbaa and the Candies
Pumbaa has 11 chocolate candies and 13 toffee candies. Each time he can eat either two candies of different types,
Sources:
or three candies of the same type. What is the largest number of candies that Pumbaa can eat according to these rules? -
Circle and Three Points
A circle is drawn on the board, and three points are marked on it in the following colors (clockwise): green, blue
and red. Jonathan is playing the following game – in each step he can do one of the following:
a) Choose two adjacent points with different colors and draw a point between them in one of these two colors
only.
b) Choose two adjacent points with identical colors and draw a point between them in any color.
c) Choose three adjacent points where at least two of them are the same color, and erase the middle one.Can Jonathan reach a state where there are three points left on the board in the following colors (clockwise): blue, green, red? Justify your answer.
Sources:- Gillis Mathematical Olympiad, 2015-2016 Question 4
-
A 2022x2022 Board and Inversion Operations
We have a `2022 times 2022` board with real numbers.
In each move, we can choose a row or a column and a real number `c`.
Then, we replace each number in the row or column from `x` to `c - x`.
Is it possible to get from any board to any other board?
-
Two Hashes
What is the maximum number of "domino" shapes (rectangles `1 times 2` or `2 times 1`) that can be placed inside the orange shape,
such that they do not overlap and do not extend beyond the boundaries of the shape?
Sources:
-
Equality in Stages
The numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 are written on the board, and David is supposed to change them in stages. At each stage, David is allowed to choose two numbers and change them by 1, that is, to add 1 to both, subtract 1 from both, or add 1 to one and subtract 1 from the other.
Can David, after a number of stages, reach a situation where all the numbers on the board are equal? If so, show an example, and if not, explain your answer in detail.
Sources:Topics:Combinatorics -> Invariants Logic -> Reasoning / Logic Number Theory -> Division -> Parity (Even/Odd) Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures- Grossman Math Olympiad, 2017, Juniors Question 3
-
Question
There are 5778 extinguished lamps arranged at equal distances on a circle. Below each lamp is a button. Pressing a button changes the state of 4 lamps: the lamp next to the button, the next two lamps in the circle clockwise, and the lamp opposite the button (an extinguished lamp lights up when its state is changed, and a lit lamp is extinguished). What is the maximum number of lamps that can be lit simultaneously?
Sources:Topics:Combinatorics -> Combinatorial Geometry Combinatorics -> Invariants Logic -> Reasoning / Logic Number Theory -> Division -> Parity (Even/Odd) Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Colorings- Beno Arbel Olympiad, 2017, Grade 8 Question 8
-
THE EXCHANGE PUZZLE
Here is a rather entertaining little puzzle with moving counters. You only need twelve counters—six of one colour, marked A, C, E, G, I, and K, and the other six marked B, D, F, H, J, and L. You first place them on the diagram, as shown in the illustration, and the puzzle is to get them into regular alphabetical order, as follows:—
A B C D E F G H I J K L The moves are made by exchanges of opposite colours standing on the same line. Thus, G and J may exchange places, or F and A, but you cannot exchange G and C, or F and D, because in one case they are both white and in the other case both black. Can you bring about the required arrangement in seventeen exchanges?
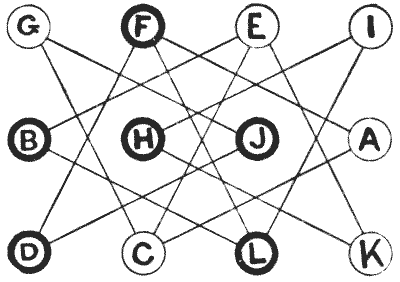
It cannot be done in fewer moves. The puzzle is really much easier than it looks, if properly attacked.
Sources:Topics:Combinatorics -> Invariants Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Puzzles and Rebuses- Amusements in Mathematics, Henry Ernest Dudeney Question 234
-
THE TWO ROOKS
This is a puzzle game for two players. Each player has a single rook. The first player places his rook on any square of the board that he may choose to select, and then the second player does the same. They now play in turn, the point of each play being to capture the opponent's rook. But in this game you cannot play through a line of attack without being captured. That is to say, if in the diagram it is Black's turn to play, he cannot move his rook to his king's knight's square, or to his king's rook's square, because he would enter the "line of fire" when passing his king's bishop's square. For the same reason he cannot move to his queen's rook's seventh or eighth squares. Now, the game can never end in a draw. Sooner or later one of the rooks must fall, unless, of course, both players commit the absurdity of not trying to win. The trick of winning is ridiculously simple when you know it. Can you solve the puzzle?
Sources:Topics:Combinatorics -> Combinatorial Geometry Combinatorics -> Invariants Combinatorics -> Game Theory Logic -> Reasoning / Logic Combinatorics -> Colorings -> Chessboard Coloring- Amusements in Mathematics, Henry Ernest Dudeney Question 393