Gillis Mathematical Olympiad, 2015-2016

  • Question 1

    Nina and Meir left their home at the same time and went to visit their grandmother. The route from their home to their grandmother's house is 3 km long, and benches are located along it.

    Nina sits on every bench along the way to eat one cookie. She eats each cookie for the same whole number of minutes. Meir also stops and sits on every bench to eat one cookie.

    It takes Meir twice as long as Nina to eat a cookie. It is also known that Nina walks at a speed of 3 km/h, and Meir at a speed of 4 km/h.

    It turned out that Meir and Nina arrived at their grandmother's house at the same time.

    How many benches were along the way? Find all the possibilities and justify your answer.

  • Question 2

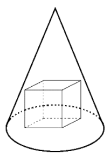
    Given a cone (with an axis of symmetry in its center, perpendicular to its base) with a height of 6 and a base that is a circle with radius `sqrt2`. A cube is inscribed within the cone – it rests on the cone's base and all its upper vertices touch the cone. Find the side length of the cube. Justify your answer.

  • Question 3

    Given a positive integer N, consider the following process: Let `S(N)` denote the sum of the digits of N. Take the sum of the digits of `S(N)`. Repeat this operation until a single-digit number is obtained. We call the number of times we performed the above process until we obtained a single-digit number the "depth" of N. For example, the depth of 49 is `S(49)=13 -> S(13)=4`, the operation was performed twice (and the depth of 45 is 1).

    a) Prove that for every number N there is indeed a finite depth, that is, a single-digit number is always obtained at some stage of the process.

    b) Let `x(n)` denote the minimum number (with the smallest value) with depth N. Find the remainder of `x(5776)` when divided by 6. Justify your answer!

    c) Find the remainder of the number `x(5776) - x(5708)` when divided by 2016. Justify your answer!

  • Question 4 - Circle and Three Points

    A circle is drawn on the board, and three points are marked on it in the following colors (clockwise): green, blue
    and red. Jonathan is playing the following game – in each step he can do one of the following:
    a) Choose two adjacent points with different colors and draw a point between them in one of these two colors
    only.
    b) Choose two adjacent points with identical colors and draw a point between them in any color.
    c) Choose three adjacent points where at least two of them are the same color, and erase the middle one.

    Can Jonathan reach a state where there are three points left on the board in the following colors (clockwise): blue, green, red? Justify your answer.

  • Question 5 - Fibonacci Polynomial

    The Fibonacci sequence is defined by `F_1 = F_2 = 1` and the recurrence relation `F_n = F_{n-1} + F_{n-2}` for every integer `n >= 3`. Given natural numbers `m,n >= 1`, find the minimum degree `d` such that there exists a polynomial `f(x) = a_d x^d + a_{d-1} x^{d-1} + ... + a_1 x + a_0` satisfying `f(k) = F_{m+k}` for all `k = 0,1,...,n`. Justify your answer.