Algebra, Word Problems, Motion Problems
Motion problems are word problems involving objects moving at constant or varying speeds. They typically use the relationship: distance = speed × time. Questions involve calculating one of these quantities, or dealing with relative speeds, meeting points, or round trips.
-
Question
The journey from home to school takes Yossi `20` minutes. One day, when Yossi was already on his way to school, he remembered that he had forgotten his pen at home. If he continues to school now, he will arrive `3` minutes before the bell. And if he goes back home to get the pen, he will be `7 ` minutes late for class. What fraction of the way to school had Yossi traveled when he remembered that he didn't have a pen?
Note: Yossi walks at a constant speed the entire time.
Sources: -
The Restless Fly
Cities A and B are 300 kilometers apart. Two cyclists start simultaneously from A and B, heading towards each other. Their speeds are constant and equal to `30` km/h and `20` km/h, respectively. At the same moment, a fly departs from city A, flying at a speed of `100` km/h. The fly overtakes the first cyclist and flies until it meets the cyclist who left from city B. The moment the fly meets the cyclist, it immediately turns around and flies back until it meets the first cyclist again, and then it turns around again, and so on, until the cyclists meet. How many kilometers did the fly travel?
Topics:Arithmetic Algebra -> Equations Logic -> Reasoning / Logic Algebra -> Word Problems -> Motion Problems -
Question
At `12:00`, the two hands of a clock coincide. In exactly how much time will they coincide again? How many times within a 24-hour period will they coincide?
-
Question
How long will it take a train traveling at a speed of `60` km/h and with a length of `50` meters to pass through a tunnel with a length of `50` meters?
Topics:Arithmetic Logic -> Reasoning / Logic Algebra -> Word Problems -> Motion Problems Units of Measurement -
Question
Nina and Meir left their home at the same time and went to visit their grandmother. The route from their home to their grandmother's house is 3 km long, and benches are located along it.
Nina sits on every bench along the way to eat one cookie. She eats each cookie for the same whole number of minutes. Meir also stops and sits on every bench to eat one cookie.
It takes Meir twice as long as Nina to eat a cookie. It is also known that Nina walks at a speed of 3 km/h, and Meir at a speed of 4 km/h.
It turned out that Meir and Nina arrived at their grandmother's house at the same time.
How many benches were along the way? Find all the possibilities and justify your answer.
Sources:- Gillis Mathematical Olympiad, 2015-2016 Question 1
-
Horse, Camel, and Donkey in a Circle
On a circular track of length 92, there is a horse, a donkey, and a camel that start from the same point and begin walking along the circle.
The horse and the camel walk counterclockwise, and the donkey walks clockwise. The camel's speed is 1 meter per second, the donkey's is 3, and the horse's is 5.In how many seconds will all three meet again?
Note: The meeting does not necessarily have to be at the starting point
Sources:Topics:Algebra -> Word Problems -> Motion Problems -
Clock Angle
How many minutes after 7:00 will the angle between the hour and minute hands be exactly one degree for the first time?
Note: The clock hands move continuously at a constant speed.Sources:Topics:Arithmetic Algebra -> Word Problems -> Motion Problems Geometry -> Plane Geometry -> Angle Calculation -
A PUZZLING WATCH
A friend pulled out his watch and said, "This watch of mine does not keep perfect time; I must have it seen to. I have noticed that the minute hand and the hour hand are exactly together every sixty-five minutes." Does that watch gain or lose, and how much per hour? Sources:- Amusements in Mathematics, Henry Ernest Dudeney Question 59
-
THE CLUB CLOCK
One of the big clocks in the Cogitators' Club was found the other night to have stopped just when, as will be seen in the illustration, the second hand was exactly midway between the other two hands. One of the members proposed to some of his friends that they should tell him the exact time when (if the clock had not stopped) the second hand would next again have been midway between the minute hand and the hour hand. Can you find the correct time that it would happen? Sources:
Sources:
- Amusements in Mathematics, Henry Ernest Dudeney Question 62
-
THE STOP-WATCH
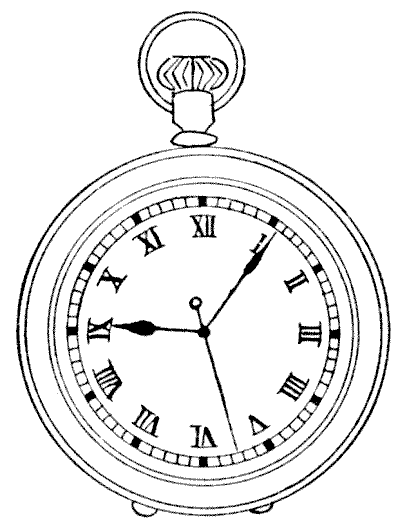 We have here a stop-watch with three hands. The second hand, which travels once round the face in a minute, is the one with the little ring at its end near the centre. Our dial indicates the exact time when its owner stopped the watch. You will notice that the three hands are nearly equidistant. The hour and minute hands point to spots that are exactly a third of the circumference apart, but the second hand is a little too advanced. An exact equidistance for the three hands is not possible. Now, we want to know what the time will be when the three hands are next at exactly the same distances as shown from one another. Can you state the time?
Sources:
We have here a stop-watch with three hands. The second hand, which travels once round the face in a minute, is the one with the little ring at its end near the centre. Our dial indicates the exact time when its owner stopped the watch. You will notice that the three hands are nearly equidistant. The hour and minute hands point to spots that are exactly a third of the circumference apart, but the second hand is a little too advanced. An exact equidistance for the three hands is not possible. Now, we want to know what the time will be when the three hands are next at exactly the same distances as shown from one another. Can you state the time?
Sources:
- Amusements in Mathematics, Henry Ernest Dudeney Question 63