Combinatorics, Case Analysis / Checking Cases, Processes / Procedures

This category covers problems involving sequences of operations or steps that evolve over time or iterations. Questions might ask about the outcome of a process, whether it terminates, or properties of its state after a certain number of steps. Often related to algorithms or invariants.

  • THE TWO PAWNS

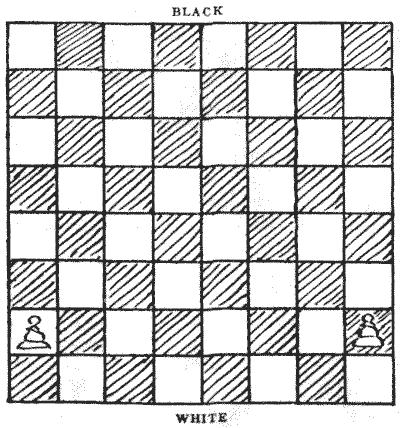    Here is a neat little puzzle in counting. In how many different ways may the two pawns advance to the eighth square? You may move them in any order you like to form a different sequence. For example, you may move the Q R P (one or two squares) first, or the K R P first, or one pawn as far as you like before touching the other. Any sequence is permissible, only in this puzzle as soon as a pawn reaches the eighth square it is dead, and remains there unconverted. Can you count the number of different sequences? At first it will strike you as being very difficult, but I will show that it is really quite simple when properly attacked.

    Sources:

  • COUNTER SOLITAIRE

    Here is a little game of solitaire that is quite easy, but not so easy as to be uninteresting. You can either rule out the squares on a sheet of cardboard or paper, or you can use a portion of your chessboard. I have shown numbered counters in the illustration so as to make the solution easy and intelligible to all, but chess pawns or draughts will serve just as well in practice.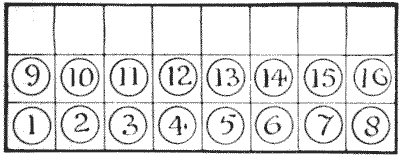 The puzzle is to remove all the counters except one, and this one that is left must be No. `1`. You remove a counter by jumping over another counter to the next space beyond, if that square is vacant, but you cannot make a leap in a diagonal direction. The following moves will make the play quite clear: `1-9`, `2-10`, `1-2`, and so on. Here `1` jumps over `9`, and you remove `9` from the board; then `2` jumps over `10`, and you remove `10`; then `1` jumps over `2`, and you remove `2`. Every move is thus a capture, until the last capture of all is made by No. `1`. Sources:

  • CHESSBOARD SOLITAIRE

    Here is an extension of the last game of solitaire. All you need is a chessboard and the thirty-two pieces, or the same number of draughts or counters. In the illustration numbered counters are used. The puzzle is to remove all the counters except two, and these two must have originally been on the same side of the board; that is, the two left must either belong to the group `1` to `16` or to the other group, `17` to `32`. You remove a counter by jumping over it with another counter to the next square beyond, if that square is vacant, but you cannot make a leap in a diagonal direction. The following moves will make the play quite clear: `3-11`, `4-12`, `3-4`, `13-3`. Here `3` jumps over `11`, and you remove `11`; `4` jumps over `12`, and you remove `12`; and so on. It will be found a fascinating little game of patience, and the solution requires the exercise of some ingenuity. Sources:

  • THE WASSAIL BOWL

    One Christmas Eve three Weary Willies came into possession of what was to them a veritable wassail bowl, in the form of a small barrel, containing exactly six quarts of fine ale. One of the men possessed a five-pint jug and another a three-pint jug, and the problem for them was to divide the liquor equally amongst them without waste. Of course, they are not to use any other vessels or measures. If you can show how it was to be done at all, then try to find the way that requires the fewest possible manipulations, every separate pouring from one vessel to another, or down a man's throat, counting as a manipulation.

    Sources:

  • THE BARRELS OF HONEY

     

    Once upon a time there was an aged merchant of Bagdad who was much respected by all who knew him. He had three sons, and it was a rule of his life to treat them all exactly alike. Whenever one received a present, the other two were each given one of equal value. One day this worthy man fell sick and died, bequeathing all his possessions to his three sons in equal shares.

    The only difficulty that arose was over the stock of honey. There were exactly twenty-one barrels. The old man had left instructions that not only should every son receive an equal quantity of honey, but should receive exactly the same number of barrels, and that no honey should be transferred from barrel to barrel on account of the waste involved. Now, as seven of these barrels were full of honey, seven were half-full, and seven were empty, this was found to be quite a puzzle, especially as each brother objected to taking more than four barrels of, the same description—full, half-full, or empty. Can you show how they succeeded in making a correct division of the property?

    Sources:

  • CROSSING THE STREAM

    During a country ramble Mr. and Mrs. Softleigh found themselves in a pretty little dilemma. They had to cross a stream in a small boat which was capable of carrying only `150` lbs. weight. But Mr. Softleigh and his wife each weighed exactly `150` lbs., and each of their sons weighed `75` lbs. And then there was the dog, who could not be induced on any terms to swim. On the principle of "ladies first," they at once sent Mrs. Softleigh over; but this was a stupid oversight, because she had to come back again with the boat, so nothing was gained by that operation. How did they all succeed in getting across? The reader will find it much easier than the Softleigh family did, for their greatest enemy could not have truthfully called them a brilliant quartette—while the dog was a perfect fool. Sources:

  • CROSSING THE RIVER AXE

    Many years ago, in the days of the smuggler known as "Rob Roy of the West," a piratical band buried on the coast of South Devon a quantity of treasure which was, of course, abandoned by them in the usual inexplicable way. Some time afterwards its whereabouts was discovered by three countrymen, who visited the spot one night and divided the spoil between them, Giles taking treasure to the value of £`800`, Jasper £`500` worth, and Timothy £`300` worth. In returning they had to cross the river Axe at a point where they had left a small boat in readiness. Here, however, was a difficulty they had not anticipated. The boat would only carry two men, or one man and a sack, and they had so little confidence in one another that no person could be left alone on the land or in the boat with more than his share of the spoil, though two persons (being a check on each other) might be left with more than their shares. The puzzle is to show how they got over the river in the fewest possible crossings, taking their treasure with them. No tricks, such as ropes, "flying bridges," currents, swimming, or similar dodges, may be employed. Sources:

  • FIVE JEALOUS HUSBANDS

    During certain local floods five married couples found themselves surrounded by water, and had to escape from their unpleasant position in a boat that would only hold three persons at a time. Every husband was so jealous that he would not allow his wife to be in the boat or on either bank with another man (or with other men) unless he was himself present. Show the quickest way of getting these five men and their wives across into safety.

    Call the men A, B, C, D, E, and their respective wives a, b, c, d, e. To go over and return counts as two crossings. No tricks such as ropes, swimming, currents, etc., are permitted.

    Sources:

  • THE FOUR ELOPEMENTS

    Colonel B—— was a widower of a very taciturn disposition. His treatment of his four daughters was unusually severe, almost cruel, and they not unnaturally felt disposed to resent it. Being charming girls with every virtue and many accomplishments, it is not surprising that each had a fond admirer. But the father forbade the young men to call at his house, intercepted all letters, and placed his daughters under stricter supervision than ever. But love, which scorns locks and keys and garden walls, was equal to the occasion, and the four youths conspired together and planned a general elopement.

    At the foot of the tennis lawn at the bottom of the garden ran the silver Thames, and one night, after the four girls had been safely conducted from a dormitory window to terra firma, they all crept softly down to the bank of the river, where a small boat belonging to the Colonel was moored. With this they proposed to cross to the opposite side and make their way to a lane where conveyances were waiting to carry them in their flight. Alas! here at the water's brink their difficulties already began.

    The young men were so extremely jealous that not one of them would allow his prospective bride to remain at any time in the company of another man, or men, unless he himself were present also. Now, the boat would only hold two persons, though it could, of course, be rowed by one, and it seemed impossible that the four couples would ever get across. But midway in the stream was a small island, and this seemed to present a way out of the difficulty, because a person or persons could be left there while the boat was rowed back or to the opposite shore. If they had been prepared for their difficulty they could have easily worked out a solution to the little poser at any other time. But they were now so hurried and excited in their flight that the confusion they soon got into was exceedingly amusing—or would have been to any one except themselves.

    As a consequence they took twice as long and crossed the river twice as often as was really necessary. Meanwhile, the Colonel, who was a very light sleeper, thought he heard a splash of oars. He quickly raised the alarm among his household, and the young ladies were found to be missing. Somebody was sent to the police-station, and a number of officers soon aided in the pursuit of the fugitives, who, in consequence of that delay in crossing the river, were quickly overtaken. The four girls returned sadly to their homes, and afterwards broke off their engagements in disgust.

    For a considerable time it was a mystery how the party of eight managed to cross the river in that little boat without any girl being ever left with a man, unless her betrothed was also present. The favourite method is to take eight counters or pieces of cardboard and mark them A, B, C, D, a, b, c, d, to represent the four men and their prospective brides, and carry them from one side of a table to the other in a matchbox (to represent the boat), a penny being placed in the middle of the table as the island.

    Readers are now asked to find the quickest method of getting the party across the river. How many passages are necessary from land to land? By "land" is understood either shore or island. Though the boat would not necessarily call at the island every time of crossing, the possibility of its doing so must be provided for. For example, it would not do for a man to be alone in the boat (though it were understood that he intended merely to cross from one bank to the opposite one) if there happened to be a girl alone on the island other than the one to whom he was engaged.

    Sources:

  • STEALING THE CASTLE TREASURE

    The ingenious manner in which a box of treasure, consisting principally of jewels and precious stones, was stolen from Gloomhurst Castle has been handed down as a tradition in the De Gourney family. The thieves consisted of a man, a youth, and a small boy, whose only mode of escape with the box of treasure was by means of a high window. Outside the window was fixed a pulley, over which ran a rope with a basket at each end. When one basket was on the ground the other was at the window. The rope was so disposed that the persons in the basket could neither help themselves by means of it nor receive help from others. In short, the only way the baskets could be used was by placing a heavier weight in one than in the other.

    Now, the man weighed `195` lbs., the youth `105` lbs., the boy `90` lbs., and the box of treasure `75` lbs. The weight in the descending basket could not exceed that in the other by more than `15` lbs. without causing a descent so rapid as to be most dangerous to a human being, though it would not injure the stolen property. Only two persons, or one person and the treasure, could be placed in the same basket at one time. How did they all manage to escape and take the box of treasure with them?

    The puzzle is to find the shortest way of performing the feat, which in itself is not difficult. Remember, a person cannot help himself by hanging on to the rope, the only way being to go down "with a bump," with the weight in the other basket as a counterpoise.

    Sources: