Minimum and Maximum Problems / Optimization Problems

These problems, also known as optimization problems, involve finding the smallest (minimum) or largest (maximum) value of a quantity or function under given constraints. Techniques can range from algebraic inequalities, geometric reasoning, to calculus (if applicable).

• MRS. PERKINS'S QUILT

  It will be seen that in this case the square patchwork quilt is built up of `169` pieces. The puzzle is to find the smallest possible number of square portions of which the quilt could be composed and show how they might be joined together. Or, to put it the reverse way, divide the quilt into as few square portions as possible by merely cutting the stitches.
  Topics:

  Geometry -> Plane Geometry Minimum and Maximum Problems / Optimization Problems Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 173

• THE MILKMAID PUZZLE

  Here is a little pastoral puzzle that the reader may, at first sight, be led into supposing is very profound, involving deep calculations. He may even say that it is quite impossible to give any answer unless we are told something definite as to the distances. And yet it is really quite "childlike and bland."

   

  In the corner of a field is seen a milkmaid milking a cow, and on the other side of the field is the dairy where the extract has to be deposited. But it has been noticed that the young woman always goes down to the river with her pail before returning to the dairy. Here the suspicious reader will perhaps ask why she pays these visits to the river. I can only reply that it is no business of ours. The alleged milk is entirely for local consumption.

  "Where are you going to, my pretty maid?"
  "Down to the river, sir," she said.
  "I'll not choose your dairy, my pretty maid."
  "Nobody axed you, sir," she said.

  
  If one had any curiosity in the matter, such an independent spirit would entirely disarm one. So we will pass from the point of commercial morality to the subject of the puzzle.

  Draw a line from the milking-stool down to the river and thence to the door of the dairy, which shall indicate the shortest possible route for the milkmaid. That is all. It is quite easy to indicate the exact spot on the bank of the river to which she should direct her steps if she wants as short a walk as possible. Can you find that spot?

  Topics:

  Minimum and Maximum Problems / Optimization Problems Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries) -> Reflection
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 187

• THE PUZZLE WALL

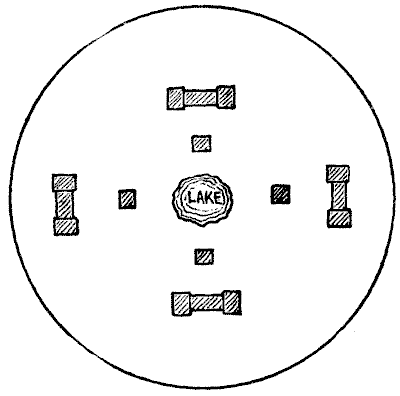  There was a small lake, around which four poor men built their cottages. Four rich men afterwards built their mansions, as shown in the illustration, and they wished to have the lake to themselves, so they instructed a builder to put up the shortest possible wall that would exclude the cottagers, but give themselves free access to the lake. How was the wall to be built?
  Topics:

  Geometry Minimum and Maximum Problems / Optimization Problems
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 192

• HOW TO MAKE CISTERNS

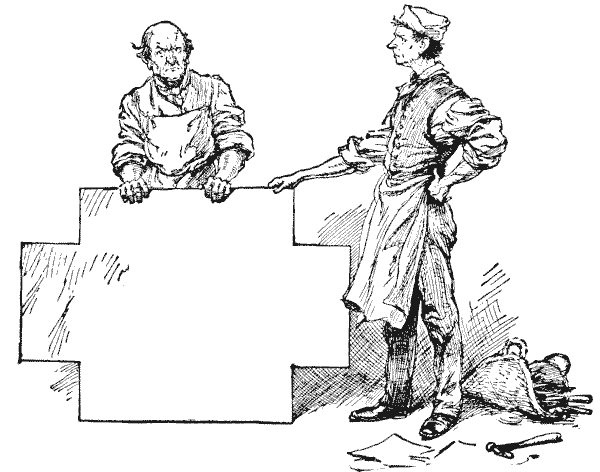  Our friend in the illustration has a large sheet of zinc, measuring (before cutting) eight feet by three feet, and he has cut out square pieces (all of the same size) from the four corners and now proposes to fold up the sides, solder the edges, and make a cistern. But the point that puzzles him is this: Has he cut out those square pieces of the correct size in order that the cistern may hold the greatest possible quantity of water? You see, if you cut them very small you get a very shallow cistern; if you cut them large you get a tall and slender one. It is all a question of finding a way of cutting put these four square pieces exactly the right size. How are we to avoid making them too small or too large?
  Topics:

  Algebra -> Word Problems Minimum and Maximum Problems / Optimization Problems
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 201

• THE CONE PUZZLE

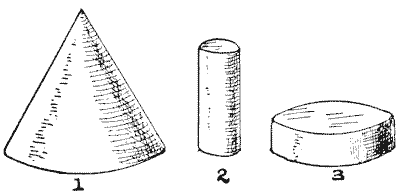  I have a wooden cone, as shown in Fig. `1`. How am I to cut out of it the greatest possible cylinder? It will be seen that I can cut out one that is long and slender, like Fig. `2`, or short and thick, like Fig. `3`. But neither is the largest possible. A child could tell you where to cut, if he knew the rule. Can you find this simple rule?
  Topics:

  Geometry -> Solid Geometry / Geometry in Space Minimum and Maximum Problems / Optimization Problems
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 202

• BISHOPS—UNGUARDED

  Place as few bishops as possible on an ordinary chessboard so that every square of the board shall be either occupied or attacked. It will be seen that the rook has more scope than the bishop: for wherever you place the former, it will always attack fourteen other squares; whereas the latter will attack seven, nine, eleven, or thirteen squares, according to the position of the diagonal on which it is placed. And it is well here to state that when we speak of "diagonals" in connection with the chessboard, we do not limit ourselves to the two long diagonals from corner to corner, but include all the shorter lines that are parallel to these. To prevent misunderstanding on future occasions, it will be well for the reader to note carefully this fact.
  Topics:

  Minimum and Maximum Problems / Optimization Problems Combinatorics -> Colorings -> Chessboard Coloring
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 297

• BISHOPS—GUARDED

  Now, how many bishops are necessary in order that every square shall be either occupied or attacked, and every bishop guarded by another bishop? And how may they be placed?
  Topics:

  Combinatorics -> Combinatorial Geometry Minimum and Maximum Problems / Optimization Problems Combinatorics -> Colorings -> Chessboard Coloring
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 298

• A PACKING PUZZLE

  As we all know by experience, considerable ingenuity is often required in packing articles into a box if space is not to be unduly wasted. A man once told me that he had a large number of iron balls, all exactly two inches in diameter, and he wished to pack as many of these as possible into a rectangular box `24` `9/10` inches long, `22` `4/5` inches wide, and `14` inches deep. Now, what is the greatest number of the balls that he could pack into that box?
  Topics:

  Geometry -> Solid Geometry / Geometry in Space Arithmetic Minimum and Maximum Problems / Optimization Problems
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 370

• STEALING THE CASTLE TREASURE

  The ingenious manner in which a box of treasure, consisting principally of jewels and precious stones, was stolen from Gloomhurst Castle has been handed down as a tradition in the De Gourney family. The thieves consisted of a man, a youth, and a small boy, whose only mode of escape with the box of treasure was by means of a high window. Outside the window was fixed a pulley, over which ran a rope with a basket at each end. When one basket was on the ground the other was at the window. The rope was so disposed that the persons in the basket could neither help themselves by means of it nor receive help from others. In short, the only way the baskets could be used was by placing a heavier weight in one than in the other.

  Now, the man weighed `195` lbs., the youth `105` lbs., the boy `90` lbs., and the box of treasure `75` lbs. The weight in the descending basket could not exceed that in the other by more than `15` lbs. without causing a descent so rapid as to be most dangerous to a human being, though it would not injure the stolen property. Only two persons, or one person and the treasure, could be placed in the same basket at one time. How did they all manage to escape and take the box of treasure with them?

  The puzzle is to find the shortest way of performing the feat, which in itself is not difficult. Remember, a person cannot help himself by hanging on to the rope, the only way being to go down "with a bump," with the weight in the other basket as a counterpoise.

  Topics:

  Algebra -> Word Problems Algorithm Theory -> Weighing Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Minimum and Maximum Problems / Optimization Problems
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 377

• THE FOOTBALL PLAYERS

  "It is a glorious game!" an enthusiast was heard to exclaim. "At the close of last season, of the footballers of my acquaintance four had broken their left arm, five had broken their right arm, two had the right arm sound, and three had sound left arms." Can you discover from that statement what is the smallest number of players that the speaker could be acquainted with?

  It does not at all follow that there were as many as fourteen men, because, for example, two of the men who had broken the left arm might also be the two who had sound right arms.

  Topics:

  Logic -> Reasoning / Logic Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Minimum and Maximum Problems / Optimization Problems
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 389