Geometry, Solid Geometry / Geometry in Space

Solid Geometry, or Geometry in Space, focuses on three-dimensional shapes such as cubes, spheres, cylinders, cones, and polyhedra. Questions typically involve calculating their surface areas and volumes, understanding their properties, and visualizing relationships between them in 3D space.

• Question

  A cube with a side length of one meter is cut into cubes with a side length of one centimeter. If all the resulting cubes are placed in a row, what will be the length of the row?

  Topics:

  Geometry -> Solid Geometry / Geometry in Space Arithmetic Algebra -> Word Problems Units of Measurement

• Question

  Given a cone (with an axis of symmetry in its center, perpendicular to its base) with a height of 6 and a base that is a circle with radius `sqrt2`. A cube is inscribed within the cone – it rests on the cone's base and all its upper vertices touch the cone. Find the side length of the cube. Justify your answer.

  

  Show hint

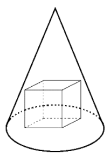  Log in here to receive the hint
  Topics:

  Geometry -> Solid Geometry / Geometry in Space Algebra -> Equations Geometry -> Plane Geometry -> Pythagorean Theorem Geometry -> Plane Geometry -> Triangles -> Triangle Similarity
  Sources:
  • Gillis Mathematical Olympiad, 2015-2016 Question 2

• Question

  The numbers `1`, `2`, `3`, ..., `8` are written on the vertices of a cube. Prove that there exists an edge of the cube such that the difference between the numbers at its endpoints is at least `3`.

  Topics:

  Geometry -> Solid Geometry / Geometry in Space Combinatorics -> Pigeonhole Principle Combinatorics -> Graph Theory Logic -> Reasoning / Logic Proof and Example -> Proof by Contradiction

• Question

  `120` identical spheres are arranged in the shape of a triangular pyramid. How many layers are there in the pyramid?

  Note: This is a pyramid, which is a three-dimensional shape, and not a triangle in a plane.

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Solid Geometry / Geometry in Space Arithmetic Logic -> Reasoning / Logic Proof and Example -> Constructing an Example / Counterexample Algebra -> Sequences -> Arithmetic Progression / Arithmetic Sequence Algebra -> Sequences -> Complete/Continue the Sequence Number Theory -> Triangular Numbers

• Question

  A cube with a side of one meter is cut into cubes with a side of one centimeter. If we put all the resulting cubes in a row, what will be the length of the row (in kilometers)?

  Topics:

  Geometry -> Solid Geometry / Geometry in Space Arithmetic Units of Measurement

• Volume of a Rectangular Prism

  Given a rectangular prism whose face areas are 6, 10, and 15. Find its volume.

  

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Solid Geometry / Geometry in Space Algebra -> Algebraic Techniques -> Roots / Radicals
  Sources:
  • Young Mathematician Olympiad, 2018-2019, Stage A, Grades 5-6 Question 4

• Game Cubes

  Aviv has game cubes, where on each of them two opposite faces are painted red and the rest are blue.
  Aviv glued a `2 times 2 times 2` cube from the game cubes. Then his friend Kfir arrived and calculated all the
  red area on the surface of the large cube. What is the largest result Kfir can get?

  Topics:

  Geometry -> Solid Geometry / Geometry in Space
  Sources:
  • Young Mathematician Olympiad, 2019-2020, Stage A, Grades 3-4 Question 6

• More Game Cubes

  Aviv has game cubes, where two opposite faces of each are painted red and the rest are blue.
  Aviv glued together a `3 xx 3 xx 3` cube from the game cubes. Then his friend Kfir came and calculated the total red area on the surface of the large cube.
  What is the largest result Kfir can get?

  Topics:

  Geometry -> Solid Geometry / Geometry in Space Combinatorics -> Combinatorial Geometry Minimum and Maximum Problems / Optimization Problems Combinatorics -> Colorings
  Sources:
  • Young Mathematician Olympiad, 2019-2020, Stage A, Grades 5-6 Question 6

• Cyclic Quadrilaterals

  Given two triangles ACE, BDF
  intersecting at 6 points: G,H,I,J,K,L
  as shown in the figure. It is given that in each of the quadrilaterals
  EFGI, DELH, CDKG, BCJL, ABIK a circle can be inscribed.
  Is it possible that a circle can also be inscribed in quadrilateral FAHJ?
  

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Solid Geometry / Geometry in Space Geometry -> Plane Geometry -> Circles Algebra -> Equations Algebra -> Inequalities Proof and Example -> Proof by Contradiction Geometry -> Plane Geometry -> Angle Calculation
  Sources:
  • Gillis Mathematical Olympiad, 2019-2020 Question 5

• THE SCULPTOR'S PROBLEM

  An ancient sculptor was commissioned to supply two statues, each on a cubical pedestal. It is with these pedestals that we are concerned. They were of unequal sizes, as will be seen in the illustration, and when the time arrived for payment a dispute arose as to whether the agreement was based on lineal or cubical measurement. But as soon as they came to measure the two pedestals the matter was at once settled, because, curiously enough, the number of lineal feet was exactly the same as the number of cubical feet. The puzzle is to find the dimensions for two pedestals having this peculiarity, in the smallest possible figures. You see, if the two pedestals, for example, measure respectively `3` ft. and `1` ft. on every side, then the lineal measurement would be `4` ft. and the cubical contents `28` ft., which are not the same, so these measurements will not do.
  Topics:

  Number Theory Geometry -> Solid Geometry / Geometry in Space Arithmetic -> Fractions Algebra -> Equations -> Diophantine Equations
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 130