Combinatorics, Matchings

In graph theory, a matching is a set of edges where no two edges share a common vertex. This topic explores finding maximum matchings, perfect matchings, or stable matchings in graphs, often in bipartite graphs (e.g., Hall's Marriage Theorem). Questions involve assignment or pairing problems.

• Question

  On a circle, `2016` blue points and one red point are marked. Consider all possible polygons whose vertices are at these points. Which polygons are more numerous – those that contain the red point or those whose vertices are all blue?

  Topics:

  Combinatorics -> Matchings Geometry -> Plane Geometry -> Circles
  Sources:
  • problems.ru web site

• Question

  From a chessboard, two opposite corners are removed (the squares `a1` and `h8`, for example). Can you tile the remaining board with dominoes?

  Show hint

  Log in here to receive the hint
  Topics:

  Combinatorics -> Invariants Combinatorics -> Matchings Logic -> Reasoning / Logic Number Theory -> Division -> Parity (Even/Odd) Proof and Example -> Proof by Contradiction Combinatorics -> Colorings -> Chessboard Coloring Puzzles and Rebuses

• Question

  `101` points are located on a circle. Which polygons with vertices at these points are more numerous – polygons with `51` sides or polygons with `50` sides?

  Topics:

  Combinatorics -> Binomial Coefficients and Pascal's Triangle Combinatorics -> Matchings Geometry -> Plane Geometry -> Circles

• Question

  Prove that the given shape cannot be cut into dominoes:

  

  Topics:

  Combinatorics -> Invariants Combinatorics -> Matchings Number Theory -> Division -> Parity (Even/Odd) Proof and Example -> Proof by Contradiction Combinatorics -> Colorings -> Chessboard Coloring Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems

• Question

  Can you cut the shape on the left into six shapes like the shape on the right?

  

  Topics:

  Combinatorics -> Invariants Combinatorics -> Matchings Proof and Example Combinatorics -> Colorings -> Chessboard Coloring Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry

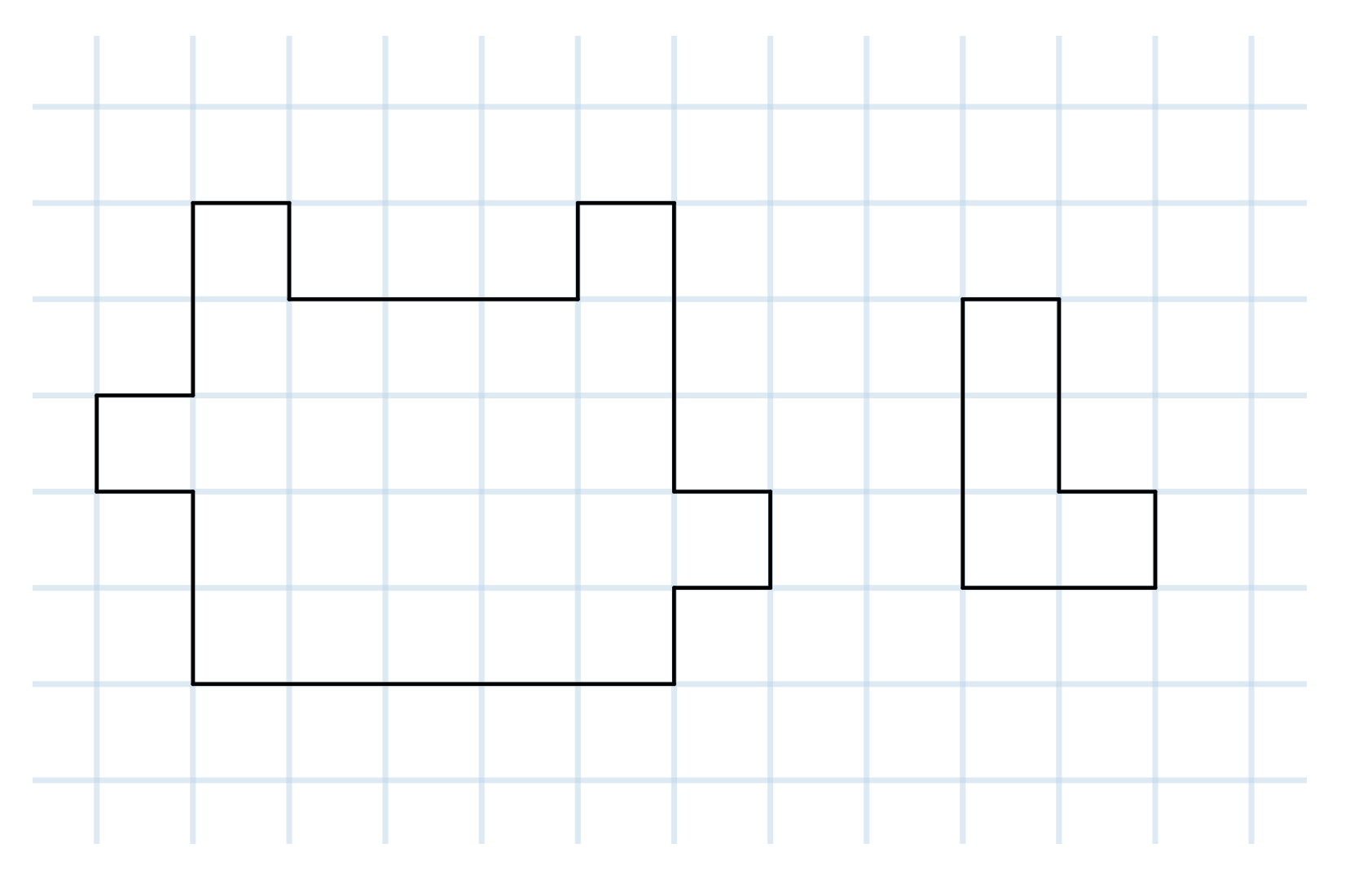
• Question

  Consider the integers from `1` to `700`.

  a. How many of these numbers are even?

  b. How many of these numbers are divisible by `7`?

  c. How many of these numbers are not divisible by `2` nor by `7`?

  Answer question c.

  Topics:

  Number Theory -> Prime Numbers Arithmetic Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules Combinatorics -> Matchings Number Theory -> Division -> Parity (Even/Odd) Number Theory -> Greatest Common Divisor (GCD) and Least Common Multiple (LCM) Set Theory

• Question

  Given `50` distinct natural numbers between `1` and `100`. It is known that no two of these numbers sum to `100`. Is it necessarily true that one of these numbers must be a perfect square?

  Topics:

  Number Theory -> Prime Numbers Arithmetic Combinatorics -> Pigeonhole Principle Combinatorics -> Matchings Logic -> Reasoning / Logic Proof and Example -> Constructing an Example / Counterexample Set Theory Combinatorics -> Case Analysis / Checking Cases -> Processes / Procedures Proof and Example -> Proof by Contradiction