Geometry, Plane Geometry, Triangles

This subject explores the properties, types (e.g., equilateral, isosceles, scalene, right-angled), and theorems related to triangles, which are fundamental three-sided polygons. Questions often involve calculating angles, side lengths, area, perimeter, and applying triangle-specific theorems.

• Question

  Inside a square ABCD with side length 1, a point E is marked, and outside the square, a point F is marked, such that triangles ABE and DAF are equilateral. Calculate the area of the pentagon CBEFD.
  

  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Triangles Geometry -> Plane Geometry -> Symmetry Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries) -> Rotation
  Sources:
  • Beno Arbel Olympiad, 2017, Grade 8 Question 6

• THE THREE VILLAGES

  I set out the other day to ride in a motor-car from Acrefield to Butterford, but by mistake I took the road going via Cheesebury, which is nearer Acrefield than Butterford, and is twelve miles to the left of the direct road I should have travelled. After arriving at Butterford I found that I had gone thirty-five miles. What are the three distances between these villages, each being a whole number of miles? I may mention that the three roads are quite straight.
  Topics:

  Geometry -> Plane Geometry -> Triangles Algebra -> Word Problems Geometry -> Plane Geometry -> Pythagorean Theorem
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 69

• THE CROSS AND THE TRIANGLE

  Cut a Greek cross into six pieces that will form an equilateral triangle. This is another hard problem, and I will state here that a solution is practically impossible without a previous knowledge of my method of transforming an equilateral triangle into a square (see No. `26`, "Canterbury Puzzles").
  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Triangles Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 144

• THE DISSECTED TRIANGLE

   

  A good puzzle is that which the gentleman in the illustration is showing to his friends. He has simply cut out of paper an equilateral triangle—that is, a triangle with all its three sides of the same length. He proposes that it shall be cut into five pieces in such a way that they will fit together and form either two or three smaller equilateral triangles, using all the material in each case. Can you discover how the cuts should be made?

  Remember that when you have made your five pieces, you must be able, as desired, to put them together to form either the single original triangle or to form two triangles or to form three triangles—all equilateral.

  Topics:

  Geometry -> Plane Geometry -> Triangles Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 156

• THE THREE RAILWAY STATIONS

  As I sat in a railway carriage I noticed at the other end of the compartment a worthy squire, whom I knew by sight, engaged in conversation with another passenger, who was evidently a friend of his.

  "How far have you to drive to your place from the railway station?" asked the stranger.

  "Well," replied the squire, "if I get out at Appleford, it is just the same distance as if I go to Bridgefield, another fifteen miles farther on; and if I changed at Appleford and went thirteen miles from there to Carterton, it would still be the same distance. You see, I am equidistant from the three stations, so I get a good choice of trains."

  Now I happened to know that Bridgefield is just fourteen miles from Carterton, so I amused myself in working out the exact distance that the squire had to drive home whichever station he got out at. What was the distance?

  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Triangles Algebra -> Word Problems
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 181

• THE YORKSHIRE ESTATES

   

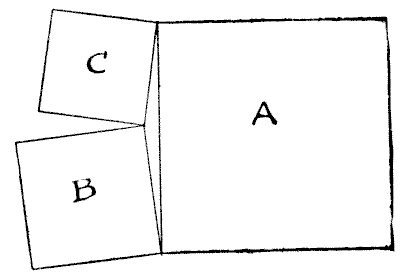
  I was on a visit to one of the large towns of Yorkshire. While walking to the railway station on the day of my departure a man thrust a hand-bill upon me, and I took this into the railway carriage and read it at my leisure. It informed me that three Yorkshire neighbouring estates were to be offered for sale. Each estate was square in shape, and they joined one another at their corners, just as shown in the diagram. Estate A contains exactly `370` acres, B contains `116` acres, and C `74` acres.

  Now, the little triangular bit of land enclosed by the three square estates was not offered for sale, and, for no reason in particular, I became curious as to the area of that piece. How many acres did it contain?

  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Triangles Geometry -> Plane Geometry -> Pythagorean Theorem
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 189

• FARMER WURZEL'S ESTATE

   

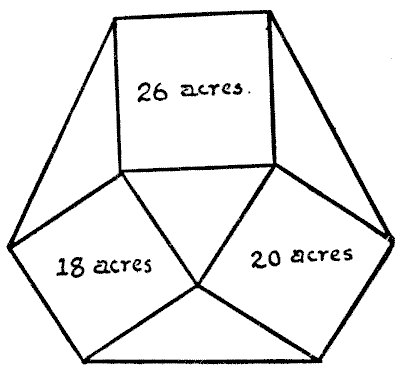
  I will now present another land problem. The demonstration of the answer that I shall give will, I think, be found both interesting and easy of comprehension.

  Farmer Wurzel owned the three square fields shown in the annexed plan, containing respectively `18, 20`, and `26` acres. In order to get a ring-fence round his property he bought the four intervening triangular fields. The puzzle is to discover what was then the whole area of his estate.

  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Triangles Geometry -> Plane Geometry -> Pythagorean Theorem
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 190

• THE TETHERED GOAT

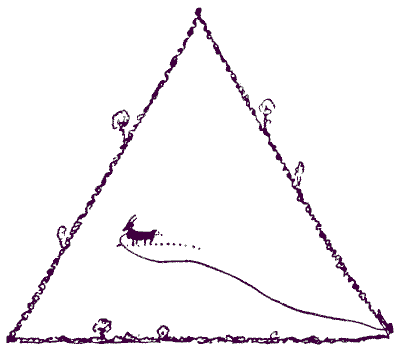  Here is a little problem that everybody should know how to solve. The goat is placed in a half-acre meadow, that is in shape an equilateral triangle. It is tethered to a post at one corner of the field. What should be the length of the tether (to the nearest inch) in order that the goat shall be able to eat just half the grass in the field? It is assumed that the goat can feed to the end of the tether.
  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Triangles Geometry -> Plane Geometry -> Angle Calculation
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 196

• PAPA'S PUZZLE

  Here is a puzzle by Pappus, who lived at Alexandria about the end of the third century. It is the fifth proposition in the eighth book of his Mathematical Collections. I give it in the form that I presented it some years ago under the title "Papa's Puzzle," just to see how many readers would discover that it was by Pappus himself. "The little maid's papa has taken two different-sized rectangular pieces of cardboard, and has clipped off a triangular piece from one of them, so that when it is suspended by a thread from the point A it hangs with the long side perfectly horizontal, as shown in the illustration. He has perplexed the child by asking her to find the point A on the other card, so as to produce a similar result when cut and suspended by a thread." Of course, the point must not be found by trial clippings. A curious and pretty point is involved in this setting of the puzzle. Can the reader discover it?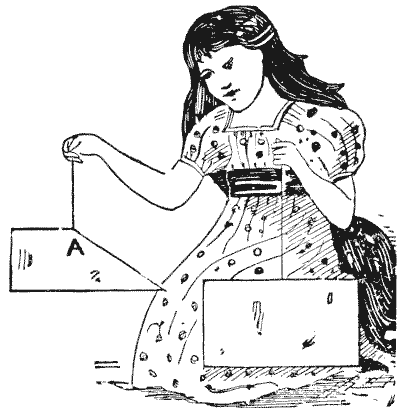
  Topics:

  Geometry -> Plane Geometry -> Triangles
  Sources:
  • Amusements in Mathematics, Henry Ernest Dudeney Question 199

• Question

  Cut a square into three parts, and then assemble them into an acute triangle with all sides of different lengths.

  Topics:

  Geometry -> Plane Geometry -> Triangles -> Triangle Congruence Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems