Geometry, Plane Geometry, Triangles, Triangle Similarity

Triangle Similarity concerns triangles that have the same shape but possibly different sizes. This means their corresponding angles are equal and corresponding sides are in proportion. Questions involve proving similarity (using AA, SSS similarity, SAS similarity criteria) and using these proportions to find unknown lengths.

• Question

  Given a cone (with an axis of symmetry in its center, perpendicular to its base) with a height of 6 and a base that is a circle with radius `sqrt2`. A cube is inscribed within the cone – it rests on the cone's base and all its upper vertices touch the cone. Find the side length of the cube. Justify your answer.

  

  Show hint

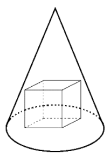  Log in here to receive the hint
  Topics:

  Geometry -> Solid Geometry / Geometry in Space Algebra -> Equations Geometry -> Plane Geometry -> Pythagorean Theorem Geometry -> Plane Geometry -> Triangles -> Triangle Similarity
  Sources:
  • Gillis Mathematical Olympiad, 2015-2016 Question 2

• Question

  Consider an arbitrary triangle. Draw tangents to the inscribed circle parallel to the sides of the triangle. These tangents cut off three smaller triangles from the original triangle. Prove that the sum of the radii of the inscribed circles of these smaller triangles is equal to the radius of the inscribed circle of the original triangle.

  Topics:

  Geometry -> Plane Geometry -> Circles -> Tangent to a Circle Geometry -> Plane Geometry -> Triangles -> Triangle Similarity