Geometry, Plane Geometry, Triangles

This subject explores the properties, types (e.g., equilateral, isosceles, scalene, right-angled), and theorems related to triangles, which are fundamental three-sided polygons. Questions often involve calculating angles, side lengths, area, perimeter, and applying triangle-specific theorems.

• Question

  Two congruent triangles form a Star of David as depicted in the drawing. Prove that the shaded area is equal to the hatched area.

  

  Show hint

  Log in here to receive the hint
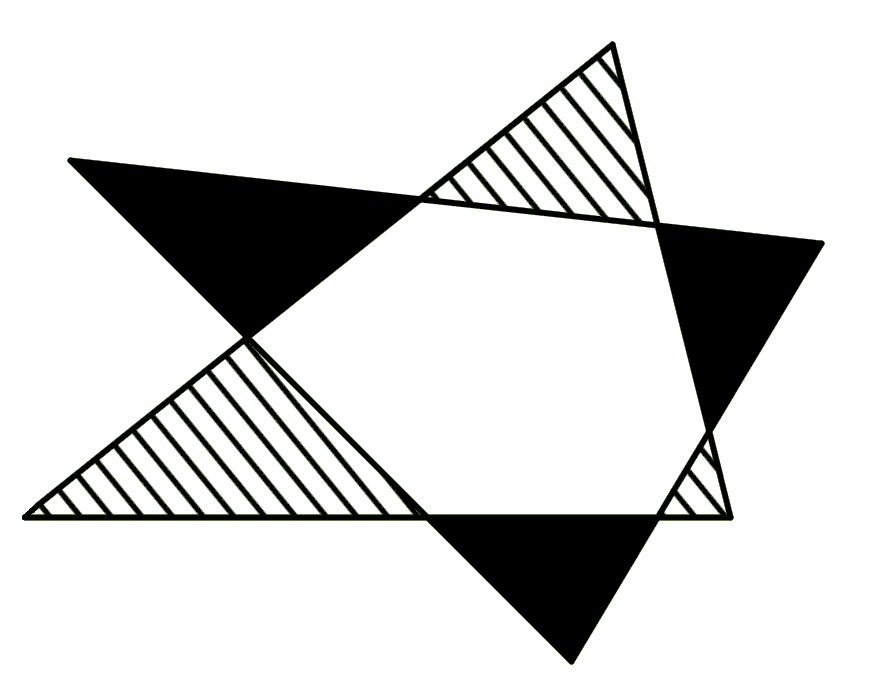  Topics:

  Geometry -> Area Calculation Proof and Example Set Theory Geometry -> Plane Geometry -> Triangles -> Triangle Congruence

• Pentagon

  In a convex pentagon `ABCDE`, the following holds: `AE=AD`, `AB=AC`, and `angle CAD=angle ABE + angle AEB`.

  Let `AM` be the median to the side `BE` in the triangle `ABE`. Prove that `AM` is half the length of the segment `CD`.

  Topics:

  Geometry -> Plane Geometry -> Angle Calculation Geometry -> Plane Geometry -> Triangles -> Triangle Congruence Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries) -> Rotation
  Sources:
  • Tournament of Towns, 1983-1984, Fall, Practice Version, Grades 9-10 Question 2 Points 3

• Question

  Given a regular polygon with n vertices. Calculate the number of distinct (non-congruent) triangles whose vertices coincide with the vertices of the polygon.

  Show hint

  Log in here to receive the hint
  Topics:

  Combinatorics Number Theory -> Modular Arithmetic / Remainder Arithmetic -> Divisibility Rules Geometry -> Plane Geometry -> Angle Calculation Geometry -> Plane Geometry -> Triangles -> Triangle Congruence
  Sources:
  • Mink Exercises and Additional Competition Materials, 2018-2019, Exercise 4 Question 3

• Where is the point?

  In a convex hexagon ABCDEF, triangles ACE and BDF are congruent and regular. Show that the three segments connecting the midpoints of opposite sides of the hexagon intersect at one point.

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Plane Geometry -> Symmetry Geometry -> Plane Geometry -> Triangles -> Triangle Congruence Geometry -> Vectors
  Sources:
  • Gillis Mathematical Olympiad, 2019-2020 Question 3

• Triangles on Lines

  Six congruent isosceles triangles are arranged as shown in the figure.
  Show that points C, F, and M are collinear.

  

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Plane Geometry -> Angle Calculation Geometry -> Plane Geometry -> Triangles -> Triangle Congruence Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries) -> Parallel Translation / Translation
  Sources:
  • Gillis Mathematical Olympiad, 2018-2019 Question 3

• Question

  Given a cone (with an axis of symmetry in its center, perpendicular to its base) with a height of 6 and a base that is a circle with radius `sqrt2`. A cube is inscribed within the cone – it rests on the cone's base and all its upper vertices touch the cone. Find the side length of the cube. Justify your answer.

  

  Show hint

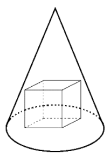  Log in here to receive the hint
  Topics:

  Geometry -> Solid Geometry / Geometry in Space Algebra -> Equations Geometry -> Plane Geometry -> Pythagorean Theorem Geometry -> Plane Geometry -> Triangles -> Triangle Similarity
  Sources:
  • Gillis Mathematical Olympiad, 2015-2016 Question 2

• Question

  Consider an arbitrary triangle. Draw tangents to the inscribed circle parallel to the sides of the triangle. These tangents cut off three smaller triangles from the original triangle. Prove that the sum of the radii of the inscribed circles of these smaller triangles is equal to the radius of the inscribed circle of the original triangle.

  Topics:

  Geometry -> Plane Geometry -> Circles -> Tangent to a Circle Geometry -> Plane Geometry -> Triangles -> Triangle Similarity