Combinatorics, Combinatorial Geometry, Cut a Shape / Dissection Problems

Dissection problems involve cutting a given geometric shape into pieces that can be rearranged to form another specified shape, or to satisfy certain conditions (e.g., forming identical pieces). Questions test spatial reasoning and understanding of area preservation.

• Question

  Dissect the given shape into four congruent parts:

  

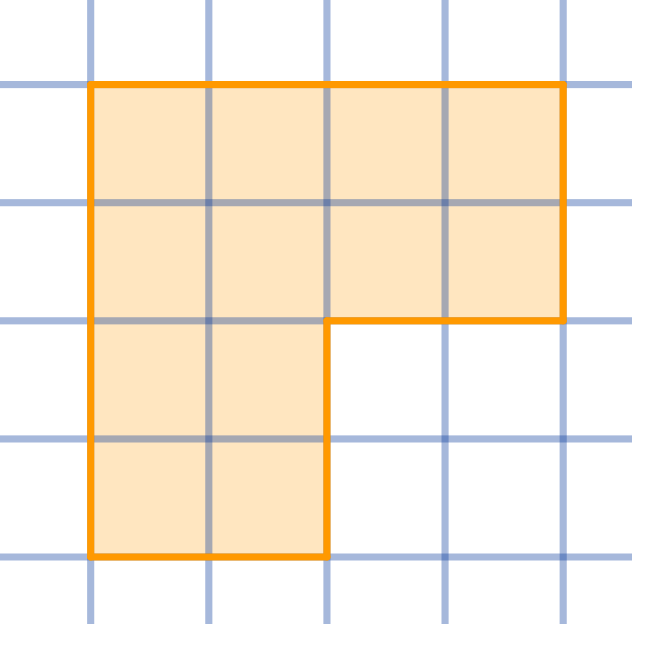  Topics:

  Geometry -> Plane Geometry -> Symmetry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry Geometry -> Plane Geometry -> Plane Transformations -> Congruence Transformations (Isometries)

• Question

  Cut the given shape into eight congruent parts:

  

  Topics:

  Geometry -> Plane Geometry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry

• Question

  Divide the given shape into 16 congruent parts:

  

  Topics:

  Geometry -> Plane Geometry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry

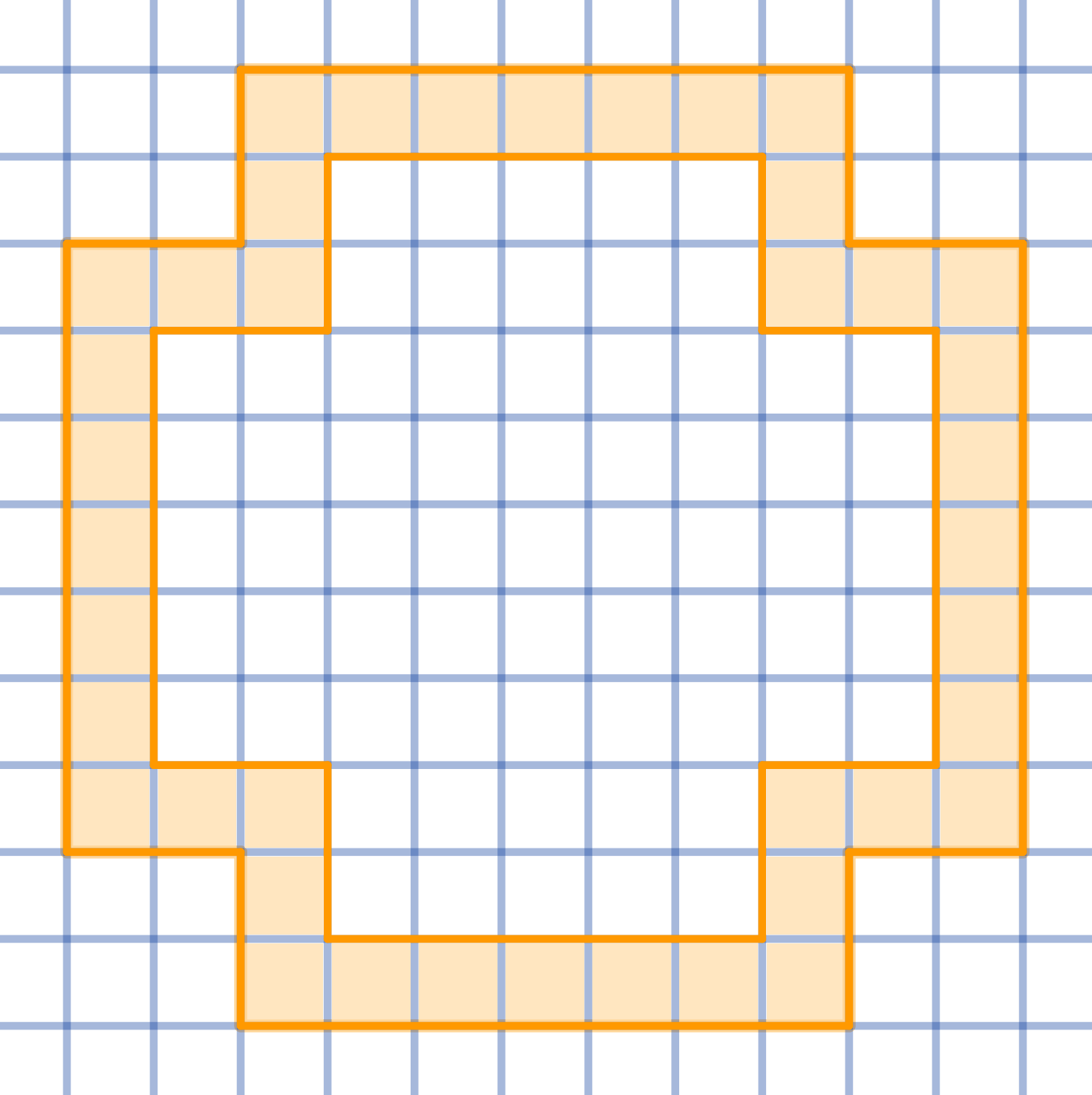
• Question

  Is it possible to cut a triangle into four convex shapes: a triangle, a quadrilateral, a pentagon, and a hexagon?

  Topics:

  Geometry -> Plane Geometry -> Triangles Proof and Example -> Constructing an Example / Counterexample Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems

• Quarter Yin-Yang

  The shape in the drawing is constructed as follows: Divide the diameter of a semicircle into two equal parts, and construct two additional semicircles on them as diameters: one inwards, and one outwards.

  

  Divide the shape into two congruent parts.

  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Circles Geometry -> Plane Geometry -> Symmetry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems

• Question

  Cut a square into three parts, and then assemble them into an acute triangle with all sides of different lengths.

  Topics:

  Geometry -> Plane Geometry -> Triangles -> Triangle Congruence Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems

• Question

  Given a sheet of paper of size `10×10` cm. Can you cut out a number of circles from this sheet such that the sum of their diameters is greater than `5` meters?

  Topics:

  Arithmetic Geometry -> Area Calculation Proof and Example -> Constructing an Example / Counterexample Minimum and Maximum Problems / Optimization Problems Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems

• Question

  Cut the given shape into "T" shapes as shown in the diagram:

  

  Topics:

  Geometry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems Combinatorics -> Combinatorial Geometry -> Grid Paper Geometry / Lattice Geometry

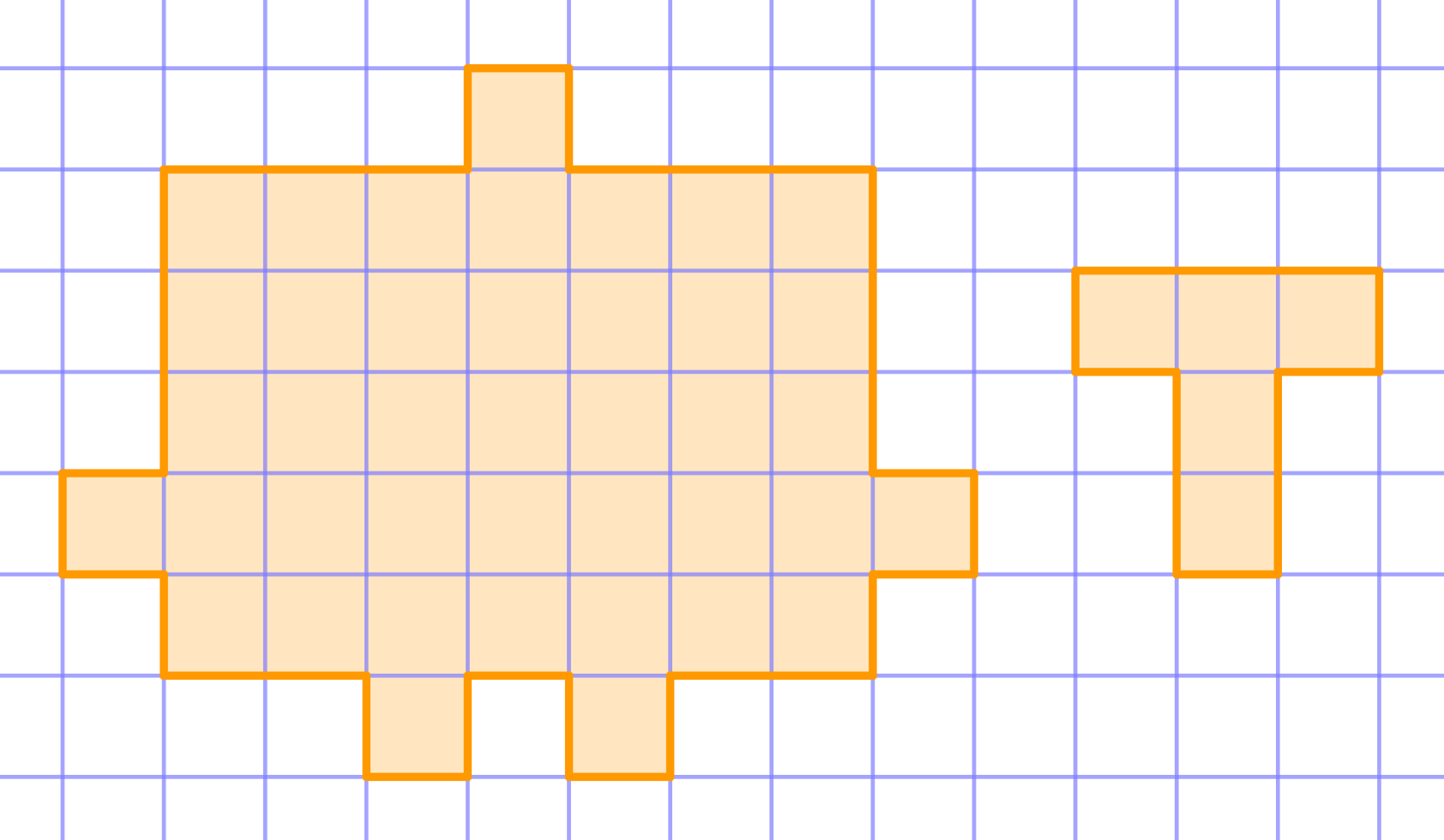
• Question

  Is there a quadrilateral that can be cut into `6` parts by two straight cuts? Justify your answer or provide an example.

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Plane Geometry Proof and Example -> Constructing an Example / Counterexample Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems

• Question

  It is known that all the angles of the given shape are right angles. Cut the shape into two polygons of equal area. You are only allowed to use an unmarked ruler.

  

  Show hint

  Log in here to receive the hint
  Topics:

  Geometry -> Area Calculation Geometry -> Plane Geometry -> Symmetry Combinatorics -> Combinatorial Geometry -> Cut a Shape / Dissection Problems